题目内容
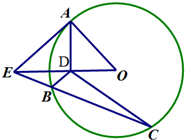 如图,AE是圆O的切线,A是切点,AD⊥OE于D,割线EC交圆O于B、C两点.
如图,AE是圆O的切线,A是切点,AD⊥OE于D,割线EC交圆O于B、C两点.(Ⅰ)证明:O,D,B,C四点共圆;
(Ⅱ)设∠DBC=50°,∠ODC=30°,求∠OEC的大小.
考点:与圆有关的比例线段
专题:直线与圆
分析:(Ⅰ)连结OA,则OA⊥EA.由已知条件利用射影定理和切割线定理推导出
=
,由此能够证明O,D,B,C四点共圆.
(Ⅱ)连结OB.∠OEC+∠OCB+∠COE=180°,能求出∠OEC的大小.
| ED |
| BD |
| EC |
| EO |
(Ⅱ)连结OB.∠OEC+∠OCB+∠COE=180°,能求出∠OEC的大小.
解答:
(Ⅰ)证明:连结OA,则OA⊥EA.
由射影定理得EA2=ED•EO.
由切割线定理得EA2=EB•EC,
∴ED•EO=EB•EC,即
=
,
又∠OEC=∠OEC,∴△BDE∽△OCE,
∴∠EDB=∠OCE.
∴O,D,B,C四点共圆.…(6分)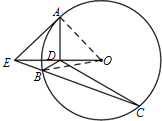
(Ⅱ)解:连结OB.因为∠OEC+∠OCB+∠COE=180°,
结合(Ⅰ)得:
∠OEC=180°-∠OCB-∠COE
=180°-∠OBC-∠DBE
=180°-∠OBC-(180°-∠DBC)
=∠DBC-∠ODC=20°.
∴∠OEC的大小为20°.…(10分)
由射影定理得EA2=ED•EO.
由切割线定理得EA2=EB•EC,
∴ED•EO=EB•EC,即
| ED |
| BD |
| EC |
| EO |
又∠OEC=∠OEC,∴△BDE∽△OCE,
∴∠EDB=∠OCE.
∴O,D,B,C四点共圆.…(6分)

(Ⅱ)解:连结OB.因为∠OEC+∠OCB+∠COE=180°,
结合(Ⅰ)得:
∠OEC=180°-∠OCB-∠COE
=180°-∠OBC-∠DBE
=180°-∠OBC-(180°-∠DBC)
=∠DBC-∠ODC=20°.
∴∠OEC的大小为20°.…(10分)
点评:本题考查四点共圆的证明,考查角的大小的求法,是中档题,解题时要认真审题,注意射影定理、切割线定理的合理运用.

练习册系列答案
相关题目
已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中的真命题是( )
| A、若m∥α,n∥β,α∥β,则m∥n |
| B、若m∥α,n∥β,α⊥β,则m⊥n |
| C、若m⊥α,n⊥β,α⊥β,则m∥n |
| D、若m⊥α,n∥β,α∥β,则m⊥n |
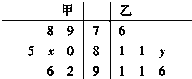 甲、乙两中学各选出7名高一学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲校学生成绩的众数是80,乙校学生成绩的中位数是86,则x+y的值为( )
甲、乙两中学各选出7名高一学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲校学生成绩的众数是80,乙校学生成绩的中位数是86,则x+y的值为( )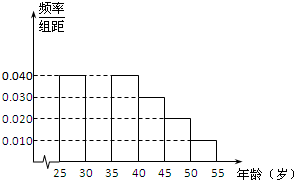 某班研究性学习小组在今年11月11日“双11购物节”期间,对[25,55)岁的人群随机抽取了1000人进行了一次是否参加“抢购商品”的调查,得到如下统计表和各年龄段人数频率分布直方图.
某班研究性学习小组在今年11月11日“双11购物节”期间,对[25,55)岁的人群随机抽取了1000人进行了一次是否参加“抢购商品”的调查,得到如下统计表和各年龄段人数频率分布直方图. 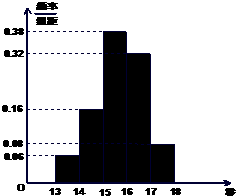 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)