题目内容
以下四个命题:
①命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”;
②设函数f(x)=x+ln(x+
),则对于任意实数a和b,“a+b<0”是“f(a)+f(b)<0”的充要条件;
③命题p:“?x∈R,x2+x+1<0”,则命题p的否定为“?x∈R,x2+x+1≥0”;
④在△ABC中,A<B是sinA<sinB的充分不必要条件;
其中真命题为( )
①命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”;
②设函数f(x)=x+ln(x+
| 1+x2 |
③命题p:“?x∈R,x2+x+1<0”,则命题p的否定为“?x∈R,x2+x+1≥0”;
④在△ABC中,A<B是sinA<sinB的充分不必要条件;
其中真命题为( )
| A、① | B、①② |
| C、①②③ | D、①②③④ |
考点:命题的真假判断与应用
专题:综合题
分析:①命题“若p则q”的逆否命题为:“若¬q,则¬p”;
②由函数是增函数,且是奇函数,可以判定该命题是正确的;
③特称命题:?x0,使P(x)的否定是:把?改为?,其它条件不变,然后否定结论,变为一个全称命题.
④在三角形中,“大角对大边,大边对大角”,结合正弦定理判定命题是否正确.
②由函数是增函数,且是奇函数,可以判定该命题是正确的;
③特称命题:?x0,使P(x)的否定是:把?改为?,其它条件不变,然后否定结论,变为一个全称命题.
④在三角形中,“大角对大边,大边对大角”,结合正弦定理判定命题是否正确.
解答:
解:①命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,是正确的;
②∵函数f(x)=x+ln(x+
)是定义域R上的增函数,且是奇函数,∴a+b<0,得a<-b,有f(a)<f(-b)=-f(b),
即f(a)+f(b)<0;反之,也成立;∴命题正确;
③命题p:“?x∈R,x2+x+1<0”,命题p的否定为“?x∈R,x2+x+1≥0”,是正确的;
④在△ABC中,
=
=
=2R(R为三角形外接圆的半径),则a=2RsinA,b=2RsinB,
由“大边对大角”,得若a>b即sinA>sinB,则A>B,
又“大角对大边”,得若A>B,即sinA>sinB,则a>b,
∴在△ABC中,A<B是sinA<sinB的充要条件,④为假命题;
∴真命题为①②③;
故选:C.
②∵函数f(x)=x+ln(x+
| 1+x2 |
即f(a)+f(b)<0;反之,也成立;∴命题正确;
③命题p:“?x∈R,x2+x+1<0”,命题p的否定为“?x∈R,x2+x+1≥0”,是正确的;
④在△ABC中,
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
由“大边对大角”,得若a>b即sinA>sinB,则A>B,
又“大角对大边”,得若A>B,即sinA>sinB,则a>b,
∴在△ABC中,A<B是sinA<sinB的充要条件,④为假命题;
∴真命题为①②③;
故选:C.
点评:本题考查了命题真假的判断与应用,四种命题间的逆否关系,充要条件,解三角形的知识,是综合题.

练习册系列答案
相关题目
设实数x、y满足
,则z=max{2x+3y-1,x+2y+2}的取值范围是( )
|
| A、[2,5] |
| B、[2,9] |
| C、[5,9] |
| D、[-1,9] |
在△ABC中,AB=AC=2,∠B=30°,P为BC边中线上的任意一点,则
•
的值为( )
| CP |
| BC |
| A、-12 | B、-6 | C、6 | D、12 |
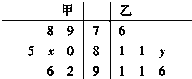 甲、乙两中学各选出7名高一学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲校学生成绩的众数是80,乙校学生成绩的中位数是86,则x+y的值为( )
甲、乙两中学各选出7名高一学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲校学生成绩的众数是80,乙校学生成绩的中位数是86,则x+y的值为( )