题目内容
20.已知函数f(x)=x+1g$\frac{x+1}{1-x}$.(1)判断并证明函数f(x)在定义城上的奇偶性;
(2)判断f(x)的单凋性(不需要证明);
(3)解不等式f(x-1)+f(2-3x)>0.
分析 (1)根据对数函数的性质求出函数的定义域即可;(2)写出函数的单调性即可;(3)根据函数的单调性得到关于x的不等式组,解出即可.
解答 解:(1)由$\frac{x+1}{1-x}$>0,解得:-1<x<1,
∴函数f(x)的定义域是(-1,1),
而f(-x)=-x+lg$\frac{-x+1}{1+x}$=-x-lg$\frac{1+x}{1-x}$=-f(x),
∴f(x)在(-1,1)上是奇函数;
(2)f(x)在(-1,1)单调递增;
(3)∵f(x-1)+f(2-3x)>0,
∴f(x-1)>f(3x-2),
∵f(x)是增函数,
∴$\left\{\begin{array}{l}{-1<x-1<1}\\{-1<3x-2<1}\\{x-1>3x-2}\end{array}\right.$,
解得:$\frac{1}{3}$<x<$\frac{1}{2}$.
点评 本题考查了函数的单调性、奇偶性,考查对数函数的性质,是一道基础题.

练习册系列答案
相关题目
15.已知a=lg$\sqrt{e}$,b=lg2e,c=e0.1,则a、b、c的大小顺序为( )
| A. | a>b>c | B. | c>b>a | C. | c>a>b | D. | b>c>a |
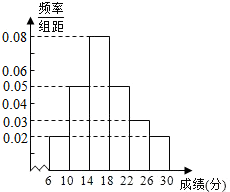 某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.