题目内容
5．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，-3）（1）求2$\overrightarrow{a}$，$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{a}•\overrightarrow{b}$；
（2）求|$\overrightarrow{a}$|，|$\overrightarrow{b}$|
分析 （1）直接利用向量的坐标运算以及数量积求解即可．
（2）直接利用向量的模求解即可．
解答 解：（1）向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，-3）
2$\overrightarrow{a}$=（2，4），$\overrightarrow{a}$+$\overrightarrow{b}$=（3，-1），$\overrightarrow{a}•\overrightarrow{b}$=2-6=-4；
（2）|$\overrightarrow{a}$|=$\sqrt{5}$，|$\overrightarrow{b}$|=$\sqrt{13}$．
点评 本题考查向量的坐标运算，考查计算能力．
练习册系列答案
相关题目
15．已知奇函数f（x）对任意正实数x1，x2（x1≠x2），恒有$\frac{{f（x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0，则一定正确的是（ ）
| A． | f（4）＞f（-6） | B． | f（-4）＜f（-6） | C． | f（-4）＞f（-6） | D． | f（4）＜f（-6） |
10．若sinα-sinβ=$\frac{\sqrt{3}}{2}$，cosα-cosβ=$\frac{1}{2}$，则cos（α-β）的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{4}$ | D． | 1 |
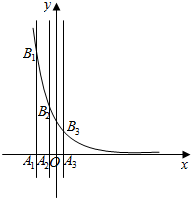（理）已知等差数列{an}的首项为p，公差为d（d＞0），对于不同的自然数n（n∈N*），直线x=an与x轴和指数函数f（x）=（$\frac{1}{2}$）x的图象分别交于点An与Bn（如图所示），记Bn的坐标为（an，bn），直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2，一般地记直角梯形AnAn+1Bn+1Bn的面积为sn．
3．对于下列表格所示的五个散点，若求得的线性回归直线方程为$\widehat{y}$=0.8x-155，
则实数m的值为8．
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |