题目内容

已知，f（x）=3cos（2x+
π
4
）+2，x∈[0，
π
2
]．
（1）求函数的值域；
（2）若方程f（x）=a有两个相异实根，求a的范围．
考点：余弦函数的图象
专题：三角函数的图像与性质
分析：（1）首先，结合所给的x的取值范围，求解2x+
π
4
∈[
π
4
，
5π
4
]，然后，结合余弦函数的图象确定其值域；
（2）结合图象进行求解．
解答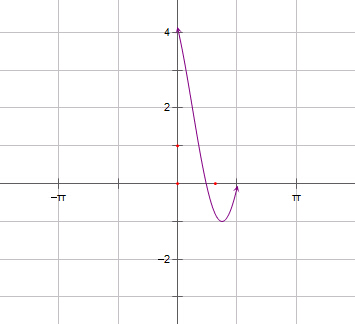： 解：（1）∵x∈[0，
π
2
]，
∴2x∈[0，π]，
∴2x+
π
4
∈[
π
4
，
5π
4
]，
∴cos（2x+
π
4
）∈[-1，
2
2
]，
∴3cos（2x+
π
4
）+2∈[-1，2+
3
2
2
]，
∴函数的值域[-1，2+
3
2
2
]，
（2）如图所示，
若方程f（x）=a有两个相异实根，
则两个函数的图象有两个交点，则
当x=
π
2
时，y=2-
3
2
2
，
∴a∈[-1，2-
3
2
2
]．
点评：本题重点考查了三角函数的图象与性质，数形结合思想在解题中的应用等知识，属于中档题．
练习册系列答案
相关题目
设集合M={x|x=（a1，a2，a3，a4，a5），ai=0，1，i=1，2，3，4，5}．若a，b∈M，定义其“距离”d（a，b）=
5
i=1
|ai-bi|；给出以下命题：
（1）M中所有元素的个数为5！；
（2）若
5
i=1
ai2=0，b1b2b3b4b5=1，则d（a，b）=5；
（3）若a，b，c∈M，则d（a，b）+d（b，c）≥d（c，a）；
（4）设W⊆M且W中任意两个元素之间的距离大于2，则|W|的最大值为4（|W|表示集合W的元素的个数）
以下命题中正确命题的序号是
 
．（写出所有正确命题的序号）
已知函数f（x）=2
3
sinxcosx-2sin2x+2（x∈R）．当x∈[0，
π
2
]时，求函数f（x）的单调递增区间．
求直线x=0，x=2，y=0与曲线y=x2所成曲边梯形的面积．
已知cos（α-
β
2
）=-
3
5
，sin（
α
2
-β）=
12
13
，α∈（
π
2
，π），β∈（0，
π
2
），求 cos（
α+β
2
）的值．
已知函数f（x）=sin
x
2
cos
x
2
-cos2
x
2
-
1
2

（Ⅰ）求函数f（x）的最小正周期和值域；
（Ⅱ）y=sinx经过如何变换得到y=f（x）；
（Ⅲ）若f（α）=
3
2
10
，求sin2α的值．
已知函数f（x）=x2-1，则f（0）=
 
，f（-2）=
 
．
记
n
1
a1
+
1
a2
+…+
1
an
为数列{an}的调和平均值，Sn为自然数列{n}的前n项和，若Hn为数列{Sn}的调和平均值，则
lim
n→∞
Hn
n
=
 
．
已知三个向量
a
，
b
，
c
不共面，且
p
=
a
+
b
-
c
，
q
=2
a
-3
b
-5
c
，
r
=-7
a
+18
b
+22
c
．试问向量
p
，
q
，
r
是否共面．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网