题目内容
在△ABC中，内角A，B，C的对边分别为a，b，c，bsinA=
acosB
（1）求角B的大小；
（2）若b=3、c=2a，求△ABC的面积．
| 3 |
（1）求角B的大小；
（2）若b=3、c=2a，求△ABC的面积．
考点：正弦定理,余弦定理
专题：计算题,三角函数的求值,解三角形
分析：（1）运用正弦定理和同角的商数关系，计算即可得到B；
（2）运用余弦定理和三角形的面积公式，计算即可得到．
（2）运用余弦定理和三角形的面积公式，计算即可得到．
解答：
解：（1）由正弦定理，bsinA=
acosB即为
sinBsinA=
sinAcosB，
由sinA＞0，即有sinB=
cosB，
tanB=
=
，
由0＜B＜π，则有B=
；
（2）由b=3，c=2a，由余弦定理，b2=c2+a2-2cacosB，
即有9=c2+a2-ac，解得a=
，c=2
．
则△ABC的面积为S=
casinB=
×2
×
×
=
．
| 3 |
sinBsinA=
| 3 |
由sinA＞0，即有sinB=
| 3 |
tanB=
| sinB |
| cosB |
| 3 |
由0＜B＜π，则有B=
| π |
| 3 |
（2）由b=3，c=2a，由余弦定理，b2=c2+a2-2cacosB，
即有9=c2+a2-ac，解得a=
| 3 |
| 3 |
则△ABC的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
3
| ||
| 2 |
点评：本题考查正弦定理、余弦定理和面积公式的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（A，ω＞0）的部分图象如图所示．（1）求函数f（x）的解析式（2）若集合{x|f（x）=m}，x∈[0，在等差数列{an}中，已知a2=3，a5=9，则数列{an}的公差d为（ ）
| A、1 | B、-1 | C、2 | D、-2 |
已知等比数列{an}的首项a1=2014，公比为q=
，记bn=a1a2a3…an，则bn达到最大值时，n的值为（ ）
| 1 |
| 2 |
| A、10 | B、11 | C、12 | D、不存在 |
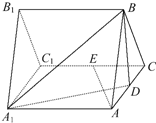如图，三棱柱ABC-A1B1C1的所有棱长都是2，又AA1⊥平面ABC，D，E分别是AC，CC1的中点．