题目内容
某校为了比较“传统式教学法”与该校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”.
(1)若全校共有学生2 000名,其中男生1 100名,现抽取100名学生对两种教学法的受欢迎程度进行问卷调查,应抽取多少名女生?
(2)表1,2分别为实行“传统式教学法”与“三步式教学法”后的数学成绩:
表1
| 数学成绩 | 90分以下 | 90~120分 | 120~140分 | 140分以上 |
| 频数 | 15 | 20 | 10 | 5 |
表2
| 数学成绩 | 90分以下 | 90~120分 | 120~140分 | 140分以上 |
| 频数 | 5 | 40 | 3 | 2 |
完成下面2×2列联表,并回答能否在犯错误的概率不超过0.01的前提下认为这两种教学法有差异.
|
| 120分以下(人数) | 120分以上(人数) | 总计(人数) |
| 一班 | |||
| 二班 | |||
| 总计 |
参考公式:K2= 其中n=a+b+c+d.
其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |
解 (1)设抽取女生x人,则 ,
,
解得x=45,所以女生抽取45人.
(2)列联表如下:
|
| 120分以下(人数) | 120分以上(人数) | 总计(人数) |
| 一班 | 35 | 15 | 50 |
| 二班 | 45 | 5 | 50 |
| 总计 | 80 | 20 | 100 |

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图.
| 组号 | 分组 | 频数 |
| 1 | [0,2) | 6 |
| 2 | [2,4) | 8 |
| 3 | [4,6) | 17 |
| 4 | [6,8) | 22 |
| 5 | [8,10) | 25 |
续表
| 6 | [10,12) | 12 |
| 7 | [12,14) | 6 |
| 8 | [14,16) | 2 |
| 9 | [16,18) | 2 |
| 合计 | 100 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组.(只需写出结论)
某车间为了规定工时定额.需要确定加工零件所需时间,为此进行了5次试验,收集到如下数据,由最小二乘法求得回归直线方程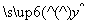 =0.67x+54.9.
=0.67x+54.9.
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(min) | 6 2 |
| 75 | 81 | 89 |
后来表中一个数据模糊不清了,请你推断出该数据为________.
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气 质量 | 优 | 良 | 轻微 污染 | 轻度 污染 | 中度 污染 | 中重度 污染 | 重度 污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为w)的关系为:
S=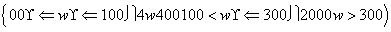 试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染.完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
|
| 非重度污染 | 重度污染 | 合计 |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 |
|
| 100 |
附:
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
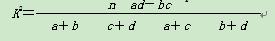
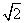
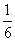 B.
B.
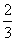 D.
D.