题目内容
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图.
| 组号 | 分组 | 频数 |
| 1 | [0,2) | 6 |
| 2 | [2,4) | 8 |
| 3 | [4,6) | 17 |
| 4 | [6,8) | 22 |
| 5 | [8,10) | 25 |
续表
| 6 | [10,12) | 12 |
| 7 | [12,14) | 6 |
| 8 | [14,16) | 2 |
| 9 | [16,18) | 2 |
| 合计 | 100 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组.(只需写出结论)
解 (1)根据频数分布表,100名学生中课外阅读时间不少于12小时的学生共有6+2+2=10名,所以样本中的学生课外阅读时间少于12小时的频率是1- =0.9.
=0.9.
从该校随机选取一名学生,估计其课外阅读时间少于12小时的概率为0.9.
(2)课外阅读时间落在组[4,6)的有17人,频率为0.17, 所以a= =
= =0.085.
=0.085.
课外阅读时间落在组[8,10)的有25人,频率为0.25,所以b= =
= =0.125.
=0.125.
(3)样本中的100名学生课外阅读时间的平均数在第4组.

 阅读快车系列答案
阅读快车系列答案为了增强学生的环保意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,并将本次竞赛的成绩(得分均为整数,满分100分)整理,制成下表:
| 成绩 | [40, 50) | [50, 60) | [60, 70) | [70, 80) | [80, 90) | [90, 100] |
| 频数 | 2 | 3 | 14 | 15 | 12 | 4 |
(1)作出被抽查学生成绩的频率分布直方图;
(2)若从成绩在[40,50)中选一名学生,从成绩在[90,100]中选2名学生,共3名学生召开座谈会,求[40,50)组中学生A1和[90,100]组中学生B1同时被选中的概率.
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
|
| 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
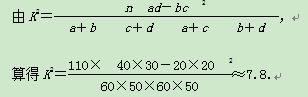 附表:
附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
某校为了比较“传统式教学法”与该校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”.
(1)若全校共有学生2 000名,其中男生1 100名,现抽取100名学生对两种教学法的受欢迎程度进行问卷调查,应抽取多少名女生?
(2)表1,2分别为实行“传统式教学法”与“三步式教学法”后的数学成绩:
表1
| 数学成绩 | 90分以下 | 90~120分 | 120~140分 | 140分以上 |
| 频数 | 15 | 20 | 10 | 5 |
表2
| 数学成绩 | 90分以下 | 90~120分 | 120~140分 | 140分以上 |
| 频数 | 5 | 40 | 3 | 2 |
完成下面2×2列联表,并回答能否在犯错误的概率不超过0.01的前提下认为这两种教学法有差异.
|
| 120分以下(人数) | 120分以上(人数) | 总计(人数) |
| 一班 | |||
| 二班 | |||
| 总计 |
参考公式:K2= 其中n=a+b+c+d.
其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |
 ,则P点的轨迹方程是__________.
,则P点的轨迹方程是__________.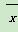 ,则( )
,则( )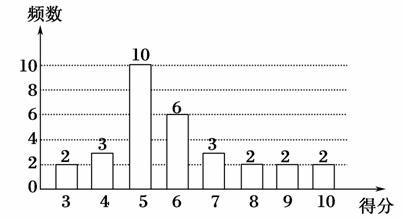
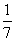 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是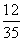 ,现从中任意取出2粒恰好是同色的概率是________.
,现从中任意取出2粒恰好是同色的概率是________.