题目内容
14.已知f′(x)是函数f(x)=xsinx的导函数,则f′($\frac{π}{2}$)的值为1.分析 先求导,再代值计算即可.
解答 解:f′(x)=sinx+xcosx,
∴f′($\frac{π}{2}$)=sin$\frac{π}{2}$+$\frac{π}{2}$cos$\frac{π}{2}$=1,
故答案为:1.
点评 本题考查了导数运算法则和导数值的求法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.空间中,直线a,b,平面α,β,下列命题正确的是( )
| A. | 若a∥α,b∥a⇒b∥α | B. | 若a∥α,b∥α,a?β,b?β⇒β∥α | ||
| C. | 若α∥β,b∥α⇒b∥β | D. | 若α∥β,a?α⇒a∥β |
2.已知命题p:函数f(x)=x2-2mx+4在[2,+∞)上单调递增;命题q:关于x的不等式mx2+2(m-2)x+1>0对任意x∈R恒成立.若p∨q为真命题,p∧q为假命题,则实数m的取值范围为( )
| A. | (1,4) | B. | [-2,4] | C. | (-∞,1]∪(2,4) | D. | (-∞,1)∪(2,4) |
6.若将函数$y=sin(x-\frac{π}{3})$图象上各点的横坐标变为原来的2倍,纵坐标不变,则所得图象对应的函数解析式为( )
| A. | $y=sin(\frac{1}{2}x-\frac{π}{3})$ | B. | $y=sin(\frac{1}{2}x-\frac{π}{6})$ | C. | $y=sin(2x-\frac{π}{3})$ | D. | $y=sin(2x-\frac{2π}{3})$ |
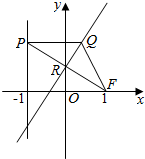 在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.