题目内容
6.已知$\overrightarrow a$=(cosθ,sinθ),$\overrightarrow b$=(-1,$\sqrt{3}$),则|$\overrightarrow a$-$2\overrightarrow b$|的最大值和最小值分别是( )| A. | 25,9 | B. | 5,3 | C. | 16,0 | D. | 16,4 |
分析 根据向量$\overrightarrow{a},\overrightarrow{b}$的坐标求出$\overrightarrow{a}-2\overrightarrow{b}=(cosθ+2,sinθ-2\sqrt{3})$,从而求出$(\overrightarrow{a}-2\overrightarrow{b})^{2}=(cosθ+2)^{2}+(sinθ-2\sqrt{3})^{2}$,根据两角差的正弦公式化简便可得出$(\overrightarrow{a}-2\overrightarrow{b})^{2}=8sin(\frac{π}{6}-θ)+17$,从而由$-1≤sin(\frac{π}{6}-θ)≤1$便可求出$(\overrightarrow{a}-2\overrightarrow{b})^{2}$的范围,进而求出$|\overrightarrow{a}-2\overrightarrow{b}|$的范围,从而得出$|\overrightarrow{a}-2\overrightarrow{b}|$的最大、最小值.
解答 解:$\overrightarrow{a}-2\overrightarrow{b}=(cosθ+2,sinθ-2\sqrt{3})$;
∴$(\overrightarrow{a}-2\overrightarrow{b})^{2}=(cosθ+2)^{2}+(sinθ-2\sqrt{3})^{2}$
=$co{s}^{2}θ+4cosθ+4+si{n}^{2}θ-4\sqrt{3}sinθ+12$
=$8(\frac{1}{2}cosθ-\frac{\sqrt{3}}{2}sinθ)+17$
=$8sin(\frac{π}{6}-θ)+17$;
∵$-1≤sin(\frac{π}{6}-θ)≤1$;
∴$9≤(\overrightarrow{a}-2\overrightarrow{b})^{2}≤25$;
∴$3≤|\overrightarrow{a}-2\overrightarrow{b}|≤5$;
∴$|\overrightarrow{a}-2\overrightarrow{b}|$的最大值为5,最小值为3.
故选:B.
点评 考查向量坐标的减法和数乘运算,以及向量数量积的计算公式及坐标运算,cos2θ+sin2θ=1,两角差的正弦公式,以及正弦函数的值域,不等式的性质.

| A. | [-1,2] | B. | [-1,+∞) | C. | [2,+∞) | D. | ∅ |
| A. |  | B. | 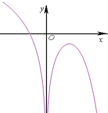 | C. | 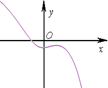 | D. |  |
| A. | -$\frac{4+\sqrt{2}}{8}$ | B. | -$\frac{4-\sqrt{2}}{8}$ | C. | -$\frac{4-\sqrt{2}}{6}$ | D. | -$\frac{4+\sqrt{2}}{6}$ |
| A. | 114 | B. | 115 | C. | 116 | D. | 117 |
| A. | 3,(-3,2) | B. | 3,(-5,4) | C. | 9,(-5,4) | D. | 9,(-3,2) |
 正方体ABCD-A1B1C1D1中,点E在棱CC1上,CE=2EC1,AB=6,M,N分别为棱AB和AD的中点.
正方体ABCD-A1B1C1D1中,点E在棱CC1上,CE=2EC1,AB=6,M,N分别为棱AB和AD的中点.