题目内容
16.在△ABC中,角A,B,C所对的边分别为a,b,c,若A=60°且$\frac{c}{b}$=$\frac{1}{2}$+$\sqrt{3}$,则tanB=$\frac{1}{2}$.分析 由已知数据统一用b表示c和a,由余弦定理可得cosB,再由同角三角函数基本关系可得.
解答 解法一:∵在△ABC中A=60°,且$\frac{c}{b}$=$\frac{1}{2}$+$\sqrt{3}$,∴c=($\frac{1}{2}$+$\sqrt{3}$)b,
由余弦定理可得a2=b2+c2-2bccosA
=b2+($\frac{1}{2}$+$\sqrt{3}$)2b2-2b($\frac{1}{2}$+$\sqrt{3}$)×$\frac{1}{2}$=$\frac{15}{4}$b2,∴a=$\frac{\sqrt{15}}{2}$b,
再由余弦定理可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\frac{15}{4}{b}^{2}+(\frac{1}{2}+\sqrt{3})^{2}{b}^{2}-{b}^{2}}{2×\frac{\sqrt{15}}{2}b×(\frac{1}{2}+\sqrt{3})b}$=$\frac{2\sqrt{5}}{5}$,
∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{5}}{5}$,∴tanB=$\frac{sinB}{cosB}$=$\frac{1}{2}$,
解法二:△ABC中,A=$\frac{π}{3}$,
∴B+C=π-A=$\frac{2π}{3}$,
∴C=$\frac{2π}{3}$-B,
由正弦定理得:$\frac{c}{b}$=$\frac{sinC}{sinB}$=$\frac{sin(\frac{2π}{3}-B)}{sinB}$
=$\frac{\frac{\sqrt{3}}{2}cosB+\frac{1}{2}sinB}{sinB}$=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$•$\frac{1}{tanB}$=$\frac{1}{2}$+$\sqrt{3}$,
∴tanB=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查余弦定理解三角形,涉及整体代换的思想,属中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{△-4}{△+4}$ | B. | $\frac{\sqrt{△}-2}{\sqrt{△}+2}$ | C. | $\frac{△+4}{△-4}$ | D. | $\frac{\sqrt{△}+2}{\sqrt{△}-2}$ |
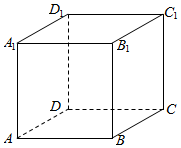 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中.
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中. 如图,椭圆的中心在原点,顶点分别是A1,A2,B1,B2,焦点分别为F1,F2,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为($\frac{\sqrt{5}-1}{2}$,1).
如图,椭圆的中心在原点,顶点分别是A1,A2,B1,B2,焦点分别为F1,F2,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为($\frac{\sqrt{5}-1}{2}$,1).