题目内容
16.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=4,$\overrightarrow a$与$\overrightarrow b$的夹角为120°,则使向量$\overrightarrow{a}$+k$\overrightarrow{b}$与k$\overrightarrow{a}$+$\overrightarrow{b}$的夹角是锐角的实数k的取值范围是($\frac{5-\sqrt{21}}{2}$,1)∪(1,$\frac{5+\sqrt{21}}{2}$).分析 利用数量积大于零解出k的范围,去掉共线的特殊情况.
解答 解:$\overrightarrow{a}•\overrightarrow{b}$=2×4×cos120°=-4.
∴($\overrightarrow{a}$+k$\overrightarrow{b}$)•(k$\overrightarrow{a}$+$\overrightarrow{b}$)=k${\overrightarrow{a}}^{2}$+k${\overrightarrow{b}}^{2}$+(k2+1)$\overrightarrow{a}•\overrightarrow{b}$=-4k2+20k-4.
∵向量$\overrightarrow{a}$+k$\overrightarrow{b}$与k$\overrightarrow{a}$+$\overrightarrow{b}$的夹角是锐角,∴-4k2+20k-4>0.解得$\frac{5-\sqrt{21}}{2}$<k<$\frac{5+\sqrt{21}}{2}$.
若向量$\overrightarrow{a}$+k$\overrightarrow{b}$与k$\overrightarrow{a}$+$\overrightarrow{b}$方向相同,则$\frac{1}{k}=k>0$,则k=1.
k的取值范围是($\frac{5-\sqrt{21}}{2}$,1)∪(1,$\frac{5+\sqrt{21}}{2}$).
故答案为($\frac{5-\sqrt{21}}{2}$,1)∪(1,$\frac{5+\sqrt{21}}{2}$).
点评 本题考查了平面向量的数量积及夹角计算,要特别考虑共线的特殊情况.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
6.已知向量$\overrightarrow{a}$=(1,2),则|$\overrightarrow{a}$|=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
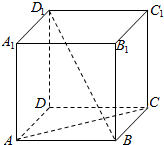 已知正方体ABCD-A1B1C1D1的棱长是a,用向量法证明AC⊥BD1.
已知正方体ABCD-A1B1C1D1的棱长是a,用向量法证明AC⊥BD1. 如图所示,三棱锥P-ABC中,∠ABC为直角,PB⊥平面ABC,AB=BC=PB=1,M为PC的中点,N为AC中点,以{$\overrightarrow{BA}$,$\overrightarrow{BC}$,$\overrightarrow{BP}$}为基底,则$\overrightarrow{MN}$的坐标为$(\frac{1}{2},0,-\frac{1}{2})$.
如图所示,三棱锥P-ABC中,∠ABC为直角,PB⊥平面ABC,AB=BC=PB=1,M为PC的中点,N为AC中点,以{$\overrightarrow{BA}$,$\overrightarrow{BC}$,$\overrightarrow{BP}$}为基底,则$\overrightarrow{MN}$的坐标为$(\frac{1}{2},0,-\frac{1}{2})$. 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,PA=BC=AC=4,D为PC的中点.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,PA=BC=AC=4,D为PC的中点.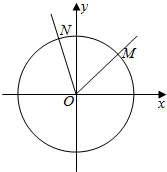 如图,在直角坐标系xOy中,锐角α的顶点是原点,始边与x轴非负半轴重合,终边交单位圆于点M(x1,y1),将角α的终边按逆时针方向旋转$\frac{π}{3}$,交单位圆于点M(x2,y2).记f(α)=y1+y2.
如图,在直角坐标系xOy中,锐角α的顶点是原点,始边与x轴非负半轴重合,终边交单位圆于点M(x1,y1),将角α的终边按逆时针方向旋转$\frac{π}{3}$,交单位圆于点M(x2,y2).记f(α)=y1+y2.