题目内容
12.已知函数f(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{f(x-1)-f(x-2),x>0}\end{array}\right.$,则f(3)的值等于-1.分析 由函数性质得f(3)=f(2)-f(1)=[f(1)-f(0)]-f(1)=-f(0),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{f(x-1)-f(x-2),x>0}\end{array}\right.$,
∴f(3)=f(2)-f(1)=[f(1)-f(0)]-f(1)=-f(0)=-(0+1)=-1.
故答案为:-1.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知f(x)是定义在[0,+∞)上单调递增的函数,则满足$f({2x-1})<f({\frac{1}{3}})$的x取值范围是( )
| A. | $({\frac{1}{2}\;,\;\;\frac{2}{3}})$ | B. | $({-∞\;,\;\;\frac{2}{3}})$ | C. | $[{\frac{1}{2}\;,\;\;\frac{2}{3}})$ | D. | $({-∞\;,\;\;\frac{2}{3}}]$ |
1.点P(2,4)关于直线x+y+1=0的对称点的坐标为( )
| A. | (5,-3) | B. | (3,-5) | C. | (-5,3) | D. | (-5,-3) |
2.已知命题p:?x∈R,log2(3x+1)≤0,则( )
| A. | ¬p:?x∈R,log2(3x+1)>0 | B. | ¬p:?x∈R,log2(3x+1)>0 | ||
| C. | ¬p:?x∈R,log2(3x+1)≤0 | D. | ¬p:?x∈R,log2(3x+1)≤0 |
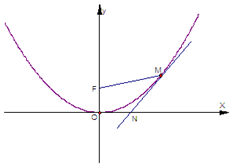 如图,抛物线x2=4y在点$M(t,\;\frac{1}{4}{t^2})\;(t>0)$处的切线与x轴相交于点N,O、F分别为该抛物线的顶点、焦点.
如图,抛物线x2=4y在点$M(t,\;\frac{1}{4}{t^2})\;(t>0)$处的切线与x轴相交于点N,O、F分别为该抛物线的顶点、焦点.