题目内容
若x,y满足
且z=y-x的最小值为-4,则k的值为( )
|
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:对不等式组中的kx-y+2≥0讨论,当k≥0时,可行域内没有使目标函数z=y-x取得最小值的最优解,k<0时,若直线kx-y+2=0与x轴的交点在x+y-2=0与x轴的交点的左边,z=y-x的最小值为-2,不合题意,由此结合约束条件作出可行域,化目标函数为直线方程的斜截式,由图得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.
解答:
解:对不等式组中的kx-y+2≥0讨论,可知直线kx-y+2=0与x轴的交点在x+y-2=0与x轴的交点的右边,
故由约束条件
作出可行域如图,
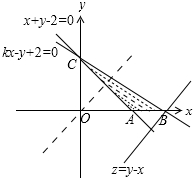
由kx-y+2=0,得x=-
,
∴B(-
,0).
由z=y-x得y=x+z.
由图可知,当直线y=x+z过B(-
,0)时直线在y轴上的截距最小,即z最小.
此时zmin=0+
=-4,解得:k=-
.
故选:D.
故由约束条件
|

由kx-y+2=0,得x=-
| 2 |
| k |
∴B(-
| 2 |
| k |
由z=y-x得y=x+z.
由图可知,当直线y=x+z过B(-
| 2 |
| k |
此时zmin=0+
| 2 |
| k |
| 1 |
| 2 |
故选:D.
点评:本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B)=( )
| A、{x|x≥0} |
| B、{x|x≤1} |
| C、{x|0≤x≤1} |
| D、{x|0<x<1} |
设命题p:?x∈R,x2+1>0,则¬p为( )
| A、?x0∈R,x02+1>0 |
| B、?x0∈R,x02+1≤0 |
| C、?x0∈R,x02+1<0 |
| D、?x∈R,x2+1≤0 |
若圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0外切,则m=( )
| A、21 | B、19 | C、9 | D、-11 |
 乒乓球台面被网分成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D,某次测试要求队员接到落点在甲上的来球后向乙回球,规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,小明回球的落点在C上的概率为
乒乓球台面被网分成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D,某次测试要求队员接到落点在甲上的来球后向乙回球,规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,小明回球的落点在C上的概率为