Question

本公司计划2009年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元，甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟，规定甲、乙两个电视台为该公司所做的每分钟广告，能给公司事来的收益分别为0.3万元和0.2万元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？

Answer 1

考点：简单线性规划的应用

专题：不等式的解法及应用

分析：设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟，总收益为z元，列出约束条件以及目标函数，画出可行域，利用线性规划求解即可．

解答： 解：设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟，总收益为z元，由题意得

x+y≤300 500x+200y≤90000 x≥0，y≥0.

目标函数为z=3000x+2000y．
二元一次不等式组等价于

x+y≤300 5x+2y≤900 x≥0，y≥0.

作出二元一次不等式组所表示的平面区域，即可行域．
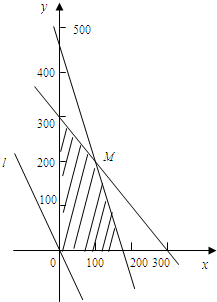
如图：作直线l：3000x+2000y=0，
即3x+2y=0．平移直线l，从图中可知，
当直线l过M点时，目标函数取得最大值．
联立

x+y=300 5x+2y=900.

解得x=100，y=200．∴点M的坐标为（100，200）．
∴z_max=3000x+2000y=700000（元）
答：该公司在甲电视台做100分钟广告，在乙电视台做200分钟广告，公司的收益最大，最大收益是70万元．

点评：本题考查线性规划的应用，正确列出约束条件，画出可行域，求出最优解是解题的关键，考查分析问题解决问题的能力．