设不等式|x-2|＜a的解集为A.且$\frac{3}{2}$∈A.$\frac{1}{2}$∉A.则a的取值范围是( )A．$\frac{1}{2}$＜a＜$\frac{3}{2}$B．$\frac{1}{2}$≤a＜$\frac{3}{2}$C．$\frac{1}{2}$＜a≤$\frac{3}{2}$D．$\frac{1}{2}$≤a≤$\frac{3} 题目和参考答案——青夏教育精英家教网——

题目内容

3．设不等式|x-2|＜a的解集为A，且$\frac{3}{2}$∈A，$\frac{1}{2}$∉A，则a的取值范围是（　　）

A．

$\frac{1}{2}$＜a＜$\frac{3}{2}$

B．

$\frac{1}{2}$≤a＜$\frac{3}{2}$

C．

$\frac{1}{2}$＜a≤$\frac{3}{2}$

D．

$\frac{1}{2}$≤a≤$\frac{3}{2}$

分析求出集合A，列出不等式组得出a的范围．

解答解：∵A为非空集合，∴a＞0，
由|x-2|＜a得-a＜x-2＜a，即2-a＜x＜2+a，
∴A=（2-a，2+a），
∵$\frac{3}{2}$∈A，$\frac{1}{2}$∉A，
∴$\left\{\begin{array}{l}{\frac{1}{2}≤2-a}\\{\frac{3}{2}＞2-a}\\{\frac{3}{2}＜2+a}\end{array}\right.$，解得$\frac{1}{2}＜a≤\frac{3}{2}$．
故选C．

点评本题考查了不等式的解法，元素与集合的关系，属于中档题．

练习册系列答案

随堂练1加2系列答案

绩优学案系列答案

作业本江西教育出版社系列答案

配套练习册系列答案

课时导学案课时作业本系列答案

指南针系列答案

新课标新精编系列答案

综合素质随堂反馈系列答案

目标复习检测卷系列答案

金种子领航考卷系列答案

相关题目

17．已知数列{a_n}中，a_n=-3n+4，等比数列{b_n}的公比q满足q=a_n-a_n-1（n≥2）且b₁=a₁，则满足$\frac{1}{{|{b_1}|}}+\frac{1}{{|{b_2}|}}+…+\frac{1}{{|{b_n}|}}＜\frac{121}{81}$成立的n的最大值为（　　）

18．已知R为实数集，集合A={x|x²-2x≥0}，B={x|x＞1}，则（∁_RA）∩B（　　）

15．若直线y=2x上存在点（x，y）满足约束条件$\left\{\begin{array}{l}{x+y+6＞0}\\{2x-y+8≥0}\\{x≤m}\end{array}\right.$，则实数m的取值范围是（　　）

（-2，+∞）

（-∞，-2）

2．定义在R上的奇函数f（x）满足f（x-2）=-f（x），且在[0，1]上是增函数，则f（$\frac{1}{4}$），f（-$\frac{1}{4}$），f（$\frac{3}{2}$）的大小关系是$f（-\frac{1}{4}）$＜$f（\frac{1}{4}）$＜$f（\frac{3}{2}）$．

8．函数$y=sin（x+\frac{π}{4}）$在闭区间（　　）上为增函数．

$[-\frac{3}{4}π，\frac{π}{4}]$

$[-\frac{π}{4}，\frac{3}{4}π]$

$[-\frac{π}{2}，\frac{π}{2}]$

15．已知向量$\overrightarrow{a}$=（sinx，-1），$\overrightarrow{b}$=$（{\sqrt{3}cosx，-\frac{1}{2}}）$．函数f（x）=（$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{a}$-2．
（1）求函数f（x）的单调递减区间；
（2）已知a，b，c分别为△ABC内角A，B，C 的对边，其中A为锐角，a=2$\sqrt{3}$，c=4，且f（A）=1，求△ABC的面积．

12．一个几何体的三视图如图所示，则这个几何体的（　　）

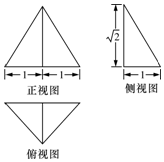
	A．	外接球的体积为12$\sqrt{3}$ π		B．	外接球的表面积为4π
	C．	体积为$\sqrt{2}$		D．	表面积为$\sqrt{5}$+$\sqrt{2}$+1

执行如图所示的程序框图，如果输入的m=15，n=12，则输出的n是（　　）