题目内容
8.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,若双曲线右支上存在一点P,满足|PF1|=6|PF2|,则该双曲线离心率的最大值为$\frac{7}{5}$.分析 运用双曲线的定义可得|PF1|-|PF2|=2a,由|PF1|=6|PF2|,可得|PF2|=$\frac{2}{5}$a,再由双曲线的性质可得|PF2|≥c-a,
解不等式结合离心率公式即可得到最大值.
解答 解:由双曲线的定义可得|PF1|-|PF2|=2a,
由|PF1|=6|PF2|,可得
|PF2|=$\frac{2}{5}$a,
又|PF2|≥c-a,
即有$\frac{2}{5}$a≥c-a,可得c≤$\frac{7}{5}$a,
即有e=$\frac{c}{a}$≤$\frac{7}{5}$,
当P为双曲线的右顶点时,e取得最大值$\frac{7}{5}$.
故答案为:$\frac{7}{5}$.
点评 本题考查双曲线的离心率的最值的求法,注意运用双曲线的定义和双曲线的性质,考查化简整理的运算能力,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
3.在区间(0,100)上任取一数x,则lg x>1的概率是( )
| A. | 0.1 | B. | 0.5 | C. | 0.8 | D. | 0.9 |
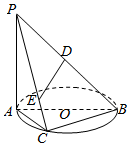 如图,AB是圆O的直径,点C是半圆的中点,PA⊥平面ABC,PA=AB,PB=6D是PB的中点,E是PC上一点.
如图,AB是圆O的直径,点C是半圆的中点,PA⊥平面ABC,PA=AB,PB=6D是PB的中点,E是PC上一点.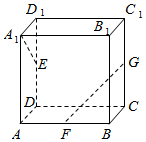 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.