题目内容
已知直线y=kx是y=2lnx的切线,则k的值为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:欲求k的值,只须求出切线的斜率的值即可,故先利用导数求出在切处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
解答:
解:∵y=2lnx,∴y'=
,
设切点为(m,2lnm),得切线的斜率为
,
∴曲线在点(m,2lnm)处的切线方程为:y-2lnm=
×(x-m).
∵过原点,∴-2lnm=-2,∴m=e,
∴k=
.
故选C.
| 2 |
| x |
设切点为(m,2lnm),得切线的斜率为
| 2 |
| m |
∴曲线在点(m,2lnm)处的切线方程为:y-2lnm=
| 2 |
| m |
∵过原点,∴-2lnm=-2,∴m=e,
∴k=
| 2 |
| e |
故选C.
点评:本小题主要考查直线的方程、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
相关题目
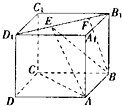 如图正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=
如图正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=| 1 |
| 2 |
| A、AC⊥BE |
| B、EF∥平面ABCD |
| C、三棱锥A-BEF的体积为定值 |
| D、△AEF的面积与△BEF的面积相等 |
下列各式中最小值为2的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、sinx+
|
下列有关命题的叙述错误的是( )
| A、对于命题P:?x∈R,x2+x+1<0,则¬P为:?x∈R,x2+x+1≥0 |
| B、若“p且q”为假命题,则p,q均为假命题 |
| C、“x>2”是“x2-3x+2>0”的充分不必要条件 |
| D、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |