题目内容
16.曲线y=$\frac{1}{5}$x5上一点M处的切线与直线y=3-x垂直,则此切线方程可能为( )| A. | 5x-5y-4=0 | B. | 5x-5y+4=0. | C. | 5x+5y-4=0 | D. | 3x+5y-4=0 |
分析 设切点(m,n),求出导数,求得切线的斜率,由两直线垂直的条件:斜率之积为-1,求得切点,由点斜式方程可得切线的方程.
解答 解:设切点M(m,n),
y=$\frac{1}{5}$x5的导数为y′=x4,
在点M处的切线斜率为m4,
由切线与直线y=3-x垂直,可得
m4=1,解得m=±1,
可得切点为(1,$\frac{1}{5}$),或(-1,-$\frac{1}{5}$),
即有切线的方程为y-$\frac{1}{5}$=x-1或y+$\frac{1}{5}$=x+1,
即为5x-5y-4=0或5x-5y+4=0.
故选:A.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,考查两直线垂直的条件:斜率之积为-1,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
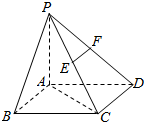 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=$\sqrt{3}$AD=$\sqrt{3}$AB=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=$\sqrt{3}$AD=$\sqrt{3}$AB=$\sqrt{3}$.