题目内容
11.在△ABC中,已知a=$\sqrt{3}$+1,b=2,C=$\frac{π}{3}$,解三角形.分析 运用余弦定理,可得c,再由正弦定理,可得A,B.
解答 解:在△ABC中,由a=$\sqrt{3}$+1,b=2,c=$\frac{π}{3}$,
运用余弦定理可得,c2=a2+b2-2abcosC
=($\sqrt{3}$+1)2+22-2($\sqrt{3}$+1)•2•$\frac{1}{2}$=6,
解得c=$\sqrt{6}$,
由正弦定理可得,$\frac{\sqrt{3}+1}{sinA}$=$\frac{2}{sinB}$=$\frac{\sqrt{6}}{\frac{\sqrt{3}}{2}}$=2$\sqrt{2}$,
即有A=$\frac{5π}{12}$,B=$\frac{π}{4}$.
点评 本题考查解三角形问题,主要考查正弦定理和余弦定理的运用,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知M(a,b)是圆O:x2+y2=r2内不在坐标轴上的一点,直线l的方程为ax+by=r2,直线m被圆O所截得的弦的中点为M,则下列说法中正确的是( )
| A. | m∥l且l与圆O相交 | B. | m⊥l且l与圆O相切 | C. | m∥l且l与圆O相离 | D. | m⊥l且l与圆O相离 |
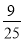 B.
B.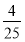 C.
C.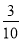 D.
D.