题目内容
11.已知等差数列{an}的前n项和为Sn,n∈N*,且a5+a6=24,S3=15.(1)求{an}的通项公式;
(2)设bn=$\frac{1}{{a}_{n}^{2}-1}$,求数列{bn}的前n项和Tn.
分析 (1)利用等差数列的通项公式及其前n项和公式即可得出;
(2)利用“裂项求和”方法即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a5+a6=24,S3=15.
∴2a1+9d=24,3a1+3d=15,
解得a1=3,d=2.
∴an=3+2(n-1)=2n+1.
(2)bn=$\frac{1}{{a}_{n}^{2}-1}$=$\frac{1}{(2n+1)^{2}-1}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$,
∴数列{bn}的前n项和Tn=$\frac{1}{4}$$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$
=$\frac{1}{4}(1-\frac{1}{n+1})$
=$\frac{n}{4(n+1)}$.
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.过点P(1,2)的直线与圆x2+y2=4相切,且与直线ax-y+1=0垂直,则实数a的值为( )
| A. | 0 | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | 0或$\frac{3}{4}$ |
6.直线y=x+m与圆C:(x+4)2+y2=8交于M、N两点,且|$\overrightarrow{MN}$|≥$\sqrt{3}$|$\overrightarrow{CM}$+$\overrightarrow{CN}$|,则实数m的取值范围是( )
| A. | [2,6] | B. | [4-$\sqrt{2}$,4+$\sqrt{2}$] | C. | [-6,-2] | D. | [-4-$\sqrt{2}$,-4+$\sqrt{2}$] |
1.抛掷一枚骰子,事件M:向上的点数是1,3,5,事件N:向上的点数是奇数,则下列不成立的是( )
| A. | M=N | B. | M⊆N | C. | N⊆M | D. | N>M |
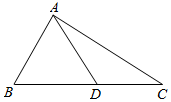 如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.
如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.