题目内容
已知函数f(x)＝|x＋1|＋|x－3|.
(1)作出函数y＝f(x)的图象；
(2)若对任意x∈R，f(x)≥a2－3a恒成立，求实数a的取值范围．
[解析] (1)①当x≤－1时，f(x)＝－x－1－x＋3＝－2x＋2；
②当－1<x<3时，f(x)＝x＋1＋3－x＝4；
③当x≥3时，f(x)＝x＋1＋x－3＝2x－2.
∴f(x)＝
∴y＝f(x)的图象如图所示．
(2)由(1)知f(x)的最小值为4，
由题意可知a2－3a≤4，即a2－3a－4≤0，
解得－1≤a≤4.故实数a的取值范围为[－1,4].
练习册系列答案
相关题目
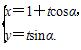(t为参数)，圆C2：ρ＝1.(极坐标轴与x轴非负半轴重合)
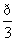时，求直线C1被圆C2所截得的弦长；
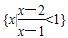，则M∩N等于( )
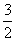} B．{x|
<x<1}
≥
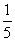|a2－a|对于x∈[2,6]恒成立，则实数a的取值范围是________．
－
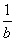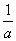＝1，则a－b<1；
－
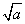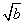|＝1，则|a－b|<1；