题目内容
已知函数f(x)=|x+1|+|x-2|-m.
(1)当m=5时,求f(x)>0的解集;
(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
[解析] (1)由题设知|x+1|+|x-2|>5,
 解得原不等式的解集为(-∞,-2)∪(3,+∞).
解得原不等式的解集为(-∞,-2)∪(3,+∞).
(2)不等式f(x)≥2即|x+1|+|x-2|≥m+2,
∵x∈R时,恒有|x+1|+|x-2|≥|(x+1)-(x-2)|=3,
不等式|x+1|+|x-2|≥m+2的解集是R,
∴m+2≤3,m的取值范围是(-∞,1].

练习册系列答案
相关题目
 的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为________.
的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为________.
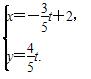 (t为参数).
(t为参数).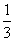 ;
;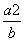 +
+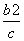 +
+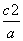 ≥1.
≥1.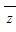 1=
1=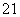 =z
=z