题目内容
已知直线C1：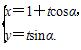
(t为参数)，圆C2：ρ＝1.(极坐标轴与x轴非负半轴重合)
(1)当α＝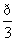
时，求直线C1被圆C2所截得的弦长；
(2)过坐标原点O作C1的垂线，垂足为A.当a变化时，求A点的轨迹的普通方程．
(1)当α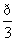＝时，C1的普通方程为y＝
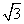(x－1)，
C2的普通方程为x2＋y2＝1.
法1：联立方程组
解得C1与C2的交点为(1,0)，(
，－
)，
所以截得的弦长为
＝1.
法2：原点O到直线C1的距离为
＝，
又圆C2的半径为1，所以截得的弦长为2
＝2×＝1.
(2)C1的普通方程为xsinα－ycosα－sinα＝0.
A点坐标为(sin2α，－cosαsinα)，
故当α变化时，A点轨迹的参数方程为
(α为参数)．
所以A点轨迹的普通方程为x2＋y2－x＝0.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，
，
，
，
，
，
，
，
，
，…，
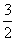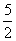…，则a2012＝________.
的⊙O中，弦AB、CD相交于点P，PA＝PB＝2，PD＝1，则圆心O到弦CD的距离为________．
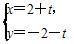(t为参数)与圆C：
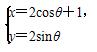(θ为参数)，则直线l的倾斜角及圆心C的直角坐标分别为( )
，(1,0) B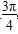
，(1,0) D.
(t为参数)，若以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C的极坐标方程为________．
＋
＝1的焦点为焦点，以直线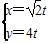
为渐近线的双曲线的参数方程为________________．
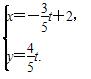(t为参数)．