题目内容
9.求经过原点,且与点P(2,1)的距离为2的直线的方程.分析 由直线经过原点与P(2,1),知:当直线的斜率k不存在时,直线方程x=0,它到原点的距离是2,成立;当直线的斜率k存在时,设直线方程为y=kx,整理,得kx-y=0,由直线与原点的距离为2,解得k,由此能得到所求的直线方程.
解答 解:∵直线经过原点与点P(2,1)距离为2,
∴当直线的斜率k不存在时,直线方程x=0,它到原点的距离是2,成立;
当直线的斜率k存在时,设直线方程为y=kx,整理,得kx-y=0,
∵直线与原点的距离为2,
∴$\frac{|2k-1|}{\sqrt{{k}^{2}+1}}$=2,解得k=$-\frac{3}{4}$,
∴直线为y=-$\frac{3}{4}$x,整理,得3x+4y=0.
故所求的直线方程为:x=0或3x+4y=0.
点评 本题考查直线方程的求法,是基础题.解题时要认真审题,注意点到直线的距离公式的应用.易错点是容易忽视直线的斜率不存在的情况.

练习册系列答案
相关题目
17.等比数列中,a1=10,q=1,则S5=( )
| A. | 10 | B. | 25 | C. | 50 | D. | 100 |
4.设偶函数f(x)的定义域为R,当x∈[0,+∞)时函数f(x)是减函数,则f(-3),f(π),f(-3.14)的大小关系为( )
| A. | f(π)=f(-3.14)>f(-3) | B. | f(π)<f(-3.14)<f(-3) | C. | f(π)>f(-3.14)>f(-3) | D. | f(π)<f(-3)<f(-3.14) |
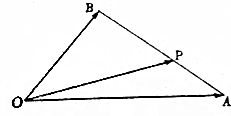 如图,在△OAB中,已知P为线段AB上的一点.|$\overrightarrow{OA}$|=4,|$\overrightarrow{OB}$|=3,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°.
如图,在△OAB中,已知P为线段AB上的一点.|$\overrightarrow{OA}$|=4,|$\overrightarrow{OB}$|=3,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°.