题目内容
12.已知函数f(x)=lg|x+9|-ax,x∈(-9,9),将f(x)表示成一个奇函数g(x)和一个偶函数h(x)的和,则偶函数h(x)的解析式为h(x)=$\frac{1}{2}lg(81-{x}^{2})$.分析 设f(x)=g(x)+h(x),其中g(x)为奇函数,h(x)为偶函数.f(-x)=g(-x)+h(-x)=-g(x)+h(x),运用函数方程的思想,求得h(x).
解答 解:设f(x)=g(x)+h(x),其中g(x)为奇函数,h(x)为偶函数.
则f(-x)=g(-x)+h(-x)=-g(x)+h(x),
∴h(x)=$\frac{1}{2}$[f(x)+f(-x)]=$\frac{1}{2}$(lg|x+9|-ax+lg|9-x|+ax)=$\frac{1}{2}lg(81-{x}^{2})$.
故答案为:h(x)=$\frac{1}{2}lg(81-{x}^{2})$.
点评 本题考查函数解析式的求解及常用方法,考查运算能力,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
6.若抛物线y2=2mx(m>0)上的点,M(3,y0)到焦点的距离是5,则y0等于( )
| A. | 2$\sqrt{3}$ | B. | 6 | C. | ±2$\sqrt{6}$ | D. | ±$\sqrt{15}$ |
20.如果A={x|x>-1},那么下列表示正确的是( )
| A. | 0⊆A | B. | {0}∈A | C. | ∅∈A | D. | {0}⊆A |
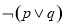 ”为假命题,则( )
”为假命题,则( ) ,
,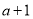 ,
,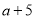 成等比数列,其倒数重新排列后为递增的等比数列
成等比数列,其倒数重新排列后为递增的等比数列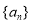 的前三项,则能使不等式
的前三项,则能使不等式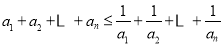 成立的自然数
成立的自然数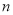 的最大值为( )
的最大值为( )