题目内容
6.若抛物线y2=2mx(m>0)上的点,M(3,y0)到焦点的距离是5,则y0等于( )| A. | 2$\sqrt{3}$ | B. | 6 | C. | ±2$\sqrt{6}$ | D. | ±$\sqrt{15}$ |
分析 由题意画出图形,利用已知结合抛物线的定义求得m,则抛物线方程可求,取x=3求得M的纵坐标.
解答  解:如图,
解:如图,
∵抛物线y2=2mx(m>0)上的点,M(3,y0)到焦点的距离是5,
∴由抛物线定义可知,M到抛物线准线x=-$\frac{m}{2}$的距离为5.
即3+$\frac{m}{2}=5$,解得:m=4.
∴抛物线方程为y2=8x,
取x=3,得${{y}_{0}}^{2}=24$,∴${y}_{0}=±2\sqrt{6}$.
故选:C.
点评 本题考查抛物线的简单性质,关键是抛物线定义的灵活运用,是中档题.

练习册系列答案
相关题目
17.定义函数f(x)=2|x+5|-|x+1|,数列a1,a2,a3…满足an+1=f(an),n∈N*.若要使a1,a2,…an,…成等差数列.则a1的取值范围为( )
| A. | a1≥-5 | B. | a1≥-1 | C. | a1≥-1或a1≤-5 | D. | 以上都不对 |
11.已知四棱锥P-ABCD的三视图如图所示,则此四棱锥的表面积为( )
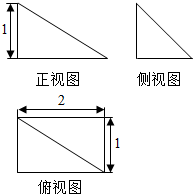

| A. | $\frac{7+2\sqrt{2}+\sqrt{5}}{2}$ | B. | $\frac{3+2\sqrt{2}+\sqrt{6}}{2}$ | C. | $\frac{7+2\sqrt{2}+6}{2}$ | D. | $\frac{3+2\sqrt{2}+\sqrt{5}}{2}$ |
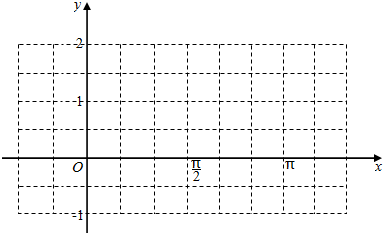
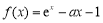 (
(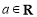 ).
).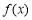 的单调区间;
的单调区间;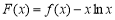 在定义域内存在零点,求
在定义域内存在零点,求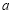 的取值范围.
的取值范围.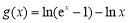 ,当
,当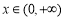 时,不等式
时,不等式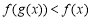 恒成立,求
恒成立,求