题目内容
4.在等差数列{an}中,a1=1,a1,a3,7a3成等比数列,记数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和为Sn.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若S1、Sm、S16成等比数列,求m的值.
分析 (Ⅰ)设等差数列{an}的公差为d,由题意可得d的方程,解方程可得数列{an}的通项公式;
(Ⅱ)列项可得$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{3}$($\frac{1}{3n-2}$-$\frac{1}{3n+1}$),可得Sn=$\frac{n}{3n+1}$,由等比数列的可得m的方程,解方程可得.
解答 解:(Ⅰ)设等差数列{an}的公差为d,
∵a1=1,a1,a3,7a3成等比数列,
∴a32=a1•7a3,∴a3=7a1,
∴1+2d=7,解得d=3,
∴数列{an}的通项公式an=1+3(n-1)=3n-2;
(Ⅱ)由(Ⅰ)可得$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(3n-2)(3n+1)}$=$\frac{1}{3}$($\frac{1}{3n-2}$-$\frac{1}{3n+1}$),
∴Sn=$\frac{1}{3}$(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+…+$\frac{1}{3n-2}$-$\frac{1}{3n+1}$)=$\frac{1}{3}$(1-$\frac{1}{3n+1}$)=$\frac{n}{3n+1}$,
∴S1=$\frac{1}{4}$,Sm=$\frac{m}{3m+1}$,S16=$\frac{16}{49}$,
∵S1、Sm、S16成等比数列,
∴($\frac{m}{3m+1}$)2=$\frac{1}{4}$×$\frac{16}{49}$,解得m=2
点评 本题考查等比数列和等差数列,涉及裂项相消法求数列的和,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.定义函数f(x)=2|x+5|-|x+1|,数列a1,a2,a3…满足an+1=f(an),n∈N*.若要使a1,a2,…an,…成等差数列.则a1的取值范围为( )
| A. | a1≥-5 | B. | a1≥-1 | C. | a1≥-1或a1≤-5 | D. | 以上都不对 |
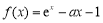 (
(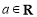 ).
).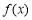 的单调区间;
的单调区间;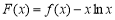 在定义域内存在零点,求
在定义域内存在零点,求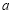 的取值范围.
的取值范围.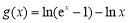 ,当
,当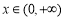 时,不等式
时,不等式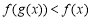 恒成立,求
恒成立,求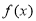 的定义域为
的定义域为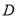 ,若存在闭区间[m,n]
,若存在闭区间[m,n] 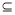 D,使得函数
D,使得函数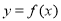 的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)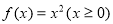 ;
; ;
; ;
;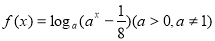 .
.