题目内容
3.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(3,-1),若向量$\overrightarrow{a}$+$\overrightarrow{b}$与m$\overrightarrow{a-}$$\overrightarrow{b}$共线,则m=-1.分析 利用已知条件求出$\overrightarrow{a}$+$\overrightarrow{b}$,m$\overrightarrow{a-}$$\overrightarrow{b}$,通过向量共线求出结果即可.
解答 解:向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(3,-1),
向量$\overrightarrow{a}$+$\overrightarrow{b}$=(4,-1),
m$\overrightarrow{a-}$$\overrightarrow{b}$=(m-3,1),
向量$\overrightarrow{a}$+$\overrightarrow{b}$与m$\overrightarrow{a-}$$\overrightarrow{b}$共线,
可得3-m=4,
解得m=-1.
故答案为:-1.
点评 本题考查向量共线定理的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.若x=1是函数f(x)=$\frac{1}{3}$m2x3+mx2+nx+p的一个极值点,则n的最大值为( )
| A. | 2 | B. | 1 | C. | 3 | D. | $\frac{9}{4}$ |
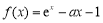 (
(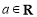 ).
).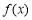 的单调区间;
的单调区间;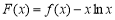 在定义域内存在零点,求
在定义域内存在零点,求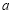 的取值范围.
的取值范围.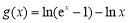 ,当
,当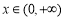 时,不等式
时,不等式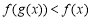 恒成立,求
恒成立,求 中,
中, ,
, 为数列
为数列 项和,则
项和,则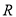 上的奇函数
上的奇函数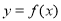 ,对于
,对于 都有
都有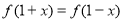 ,当
,当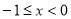 时,
时,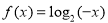 ,则函数
,则函数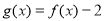 在
在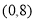 内所有的零点之和为( )
内所有的零点之和为( )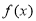 的定义域为
的定义域为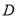 ,若存在闭区间[m,n]
,若存在闭区间[m,n] 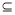 D,使得函数
D,使得函数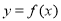 的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)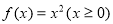 ;
; ;
; ;
; .
.