题目内容
2.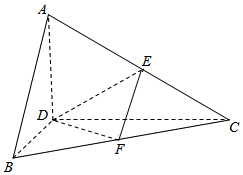 正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.(Ⅰ)试判断直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)求二面角E-DF-C的余弦值;
(Ⅲ)求四面体ABCD的外接球表面积.
分析 (Ⅰ)要证明线面平行,关键是在平面内找到一条可能与已知直线平行的直线,观察到平面BEF中三条已知直线中,EF可能与AB平行,故可以以此为切入点进行证明.
(Ⅱ)根据题意,构造空间直角坐标系,求出各点的坐标,进行求出相应直线的方向向量和平面的法向量,利用向量法,通过求两个平面法向量的夹角求二面角.
(Ⅲ)以DA,DB,DC为棱补成一个长方体,则四面体ADBC的外接球即为长方体的外接球,进而求出球的半径,利用球的表面积公式即可计算求解.
解答 解:(I)∵如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
又∵AB?平面DEF,EF?平面DEF.
∴AB∥平面DEF. …(4分)
(Ⅱ)以点D为坐标原点,直线DB、DC、DA为x轴、y轴、z轴,建立空间直角坐标系,
则A(0,0,2)B(2,0,0)C(0,2$\sqrt{3}$,0),E(0,$\sqrt{3}$,1),F(1,$\sqrt{3}$,0)
平面CDF的法向量为$\overrightarrow{DA}$=(0,0,2),设平面EDF的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{DF}•\overrightarrow{n}=0}\\{\overrightarrow{DE}•\overrightarrow{n}=0}\end{array}\right.$即$\left\{\begin{array}{l}{x+\sqrt{3}y=0}\\{\sqrt{3}y+z=0}\end{array}\right.$,取$\overrightarrow{n}$=(3,-$\sqrt{3}$,3),
cos<$\overrightarrow{DA}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{DA}•\overrightarrow{n}}{|\overrightarrow{DA}||\overrightarrow{n}|}$=$\frac{\sqrt{21}}{7}$.
所以二面角E-DF-C的余弦值为$\frac{\sqrt{21}}{7}$.…(8分)
(Ⅲ)以DA,DB,DC为棱补成一个长方体,则四面体ADBC的外接球即为长方体的外接球.
设球的半径为R,则22+22+(2$\sqrt{3}$)2=(2R)2,
∴R=$\sqrt{5}$.
于是球的表面积S=4πR2=4π×5=20π. …(12分)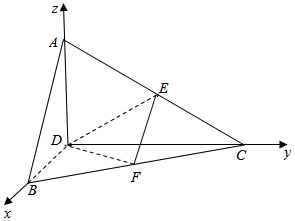
点评 本题主要考查了二面角的平面角及求法,直线与平面平行的判定,球的表面积的求法,可以用空间向量来解决,其步骤是:建立空间直角坐标系⇒明确相关点的坐标⇒明确相关向量的坐标⇒通过空间向量的坐标运算求解,属于中档题.

| A. | 零个 | B. | 一个 | C. | 二个 | D. | 无数多个 |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |