题目内容
4.求函数y=lnx-x3+2x的导数.分析 直接根据基本初等函数的导数公式得,(lnx)'=$\frac{1}{x}$;(x3)'=3x2;(2x)'=2xln2,再四则运算即可.
解答 解:根据基本初等函数的导数公式得,
(lnx)'=$\frac{1}{x}$;
(x3)'=3x2;
(2x)'=2xln2,
再由导数的四则运算法则得,
原函数的导数为y'=$\frac{1}{x}$-3x2+2xln2.
点评 本题主要考查了基本初等函数的导数的求解,涉及对数函数,幂函数和指数函数的导数,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
15.若s,t均为正数,且s+t=1,则$\frac{st}{(st+1)(st+4)}$的最大值是( )
| A. | $\frac{4}{85}$ | B. | $\frac{7}{72}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{7}$ |
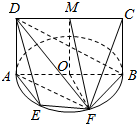 如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.
如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.