题目内容
1.向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 0 | D. | $-\frac{{\sqrt{3}}}{2}$ |
分析 根据平面向量数量积的运算公式求出$\overrightarrow{a}$、$\overrightarrow{b}$夹角的余弦值,再根据向量投影的定义写出运算结果.
解答 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,
∴${\overrightarrow{a}}^{2}$+$\overrightarrow{a}$•$\overrightarrow{b}$=12+1×2×cosθ=0,θ为$\overrightarrow{a}$、$\overrightarrow{b}$的夹角;
∴cosθ=-$\frac{1}{2}$;
∴$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为|$\overrightarrow{a}$|cosθ=1×(-$\frac{1}{2}$)=-$\frac{1}{2}$.
故选:B.
点评 本题考查了平面向量数量积和向量投影的定义与应用问题,是基础题目.

练习册系列答案
相关题目
12.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x≤0}\\{-lnx,x>0}\end{array}\right.$若关于x的方程f2(x)+f(x)+m=0有三个不同实数根,则m的取值范围是( )
| A. | $m<\frac{1}{4}$ | B. | m≤-2 | C. | $-2≤m<\frac{1}{4}$ | D. | m>2 |
16.过正方体中心的平面截正方体所得的截面中,不可能的图形是( )
| A. | 三角形 | B. | 长方形 | ||
| C. | 对角线不相等的菱形 | D. | 六边形 |
6.将函数$f(x)=3sin({3x-\frac{π}{4}})$的图象向左平移$\frac{π}{4}$个单位,再向下平移4个单位,得到函数g(x)的图象,则函数f(x)的图象与函数g(x)的图象( )
| A. | 关于点(-2,0)对称 | B. | 关于点(0,-2)对称 | ||
| C. | 关于直线x=-2对称 | D. | 关于直线x=0对称 |
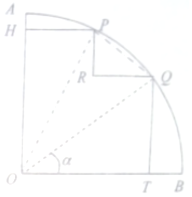 现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?
现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?