题目内容
15.已知f(x)=$\left\{\begin{array}{l}{x^2}-2ax,x≥2\\ 4x-6,x<2\end{array}$在定义域R上是增函数,则a的取值范围是( )| A. | a≥0 | B. | a≤0 | C. | $a≤\frac{1}{2}$ | D. | a≤-1 |
分析 由题意可知当x<2时,f(x)=4x-6,在(-∞,2)单调递增,恒成立,当x≥2时,由f(x)=x2-2ax,由二次函数的图象及性质可知:$\left\{\begin{array}{l}{-\frac{-2a}{2}≤2}\\{4×2-4a≥4×2-6}\end{array}\right.$,即可求得a的取值范围.
解答 解:由题意可知:当x<2时,f(x)=4x-6,在(-∞,2)单调递增,恒成立,
当x≥2时,由f(x)=x2-2ax,
由二次函数的图象及性质可知:函数在[2,+∞)单调递增,
则对称轴x=-$\frac{-2a}{2}$≤2,f(2)≥4×2-6,
∴$\left\{\begin{array}{l}{-\frac{-2a}{2}≤2}\\{4×2-4a≥4×2-6}\end{array}\right.$,整理得:$\left\{\begin{array}{l}{a≤2}\\{4a≤2}\end{array}\right.$,解得:a≤$\frac{1}{2}$,
a的取值范围为a≤$\frac{1}{2}$,
故选C.
点评 本题考查二次函数图象及性质,考查分段函数的单调性与二次函数单调性的应用,考查分类讨论思想,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
10.已知函数f(x)=ln$\frac{x}{2}$+$\frac{1}{2}$,g(x)=ex-2,对于?m∈R,?n∈(0,+∞)使得f(m)=g(n)成立,则n-m的最大值为( )
| A. | -ln2 | B. | ln2 | C. | 2$\sqrt{e}$-3 | D. | e2-3 |
6.某射击运动员进行打靶练习,已知打十枪每发的靶数为9,10,7,8,10,10,6,8,9,7,设其平均数为a,中位数为b,众数为c,则有( )
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c>b>a |
3.复数z满足(1-i)z=m+i (m∈R,i为虚数单位),在复平面上z对应的点不可能在 ( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.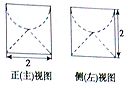 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )
 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )| A. | 2π | B. | $\frac{4π}{3}$ | C. | π | D. | $\frac{π}{2}$ |
5.某几何体的三视图如图所示,这几何体为( )


| A. | 长方体 | B. | 圆柱 | C. | 圆台 | D. | 棱柱 |