题目内容
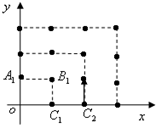2010年，我国南方省市遭遇旱涝灾害，为防洪抗旱，某地区大面积植树造林，如图，在区域{（x，y）|x≥0，y≥0}内植树，第一棵树在A1（0，1）点，第二棵树在B1（1，1）点，第三棵树在C1（，0）点，第四棵树在C2（2，0）点，接着按图中箭头方向，每隔一个单位种一颗树，那么，第2014棵树所在的点的坐标是考点：归纳推理
专题：规律型
分析：将OA1B1C1设为第一个正方形，种植3棵树，依次下去，归纳出第二个正方形，第三个正方形种植7棵树，…，得出规律，计算出前43个正方形共有多少棵树，从而得到第2014棵树所在的点的坐标．
解答：
解：OA1B1C1设为第一个正方形，种植3棵树，
依次下去，第二个正方形种植5棵树，
第三个正方形种植7棵树，
…
它们构成一个等差数列，公差为2．
故前43个正方形共有43×3+
×2=1935棵树，
又2014-1935=79，79-44=35，45-35=10，
因此第2011棵树在（10，44）点处．
故答案为：（10，44）
依次下去，第二个正方形种植5棵树，
第三个正方形种植7棵树，
…
它们构成一个等差数列，公差为2．
故前43个正方形共有43×3+
| 43×42 |
| 2 |
又2014-1935=79，79-44=35，45-35=10，
因此第2011棵树在（10，44）点处．
故答案为：（10，44）
点评：本题考点是进行简单的合情推理，由图形观察出规律是解题的重点．
练习册系列答案
相关题目
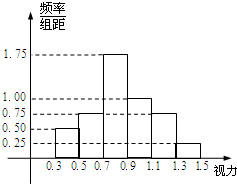从某校高三年级随机抽取一个班，对该班45名学生的高校招生体检表中视力情况进行统计，其结果的频率分布直方图如图．若某高校A专业对视力的要求在0.9以上，则该班学生中能报A专业的人数为已知平面α过点A（3，0，0），B（0，3，0），C（0，0，3），则原点O到平面α的距离为（ ）
| A、3 | ||
| B、6 | ||
C、
| ||
D、2
|
参数方程
（θ为参数）化为普通方程是（ ）
|
| A、（x-1）2+（y+3）2=1 |
| B、（x+3）2+（y-1）2=4 |
| C、（x-2）2+（y+2）2=4 |
| D、x+y-2=0 |