题目内容
2.若函数f(x)的定义域为[-1,2],则函数f(2x-1)的定义域为[0,$\frac{3}{2}$].分析 根据函数定义域的求法,直接解不等式-1≤2x-1≤2,即可求函数y=f(2x-1)的定义域.
解答 解:∵函数y=f(x)的定义域为[-1,2],
∴-1≤x≤2,
由-1≤2x-1≤2,
解得:0≤x≤$\frac{3}{2}$,
即函数y=f(2x-1)的定义域[0,$\frac{3}{2}$],
故答案为:[0,$\frac{3}{2}$].
点评 本题主要考查复合函数定义域的求法,直接利用函数f(x)的定义域,解不等式即可.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.下列命题中,是假命题的是( )
| A. | ?x>0,x>lnx | B. | ?x0∈R,tanx0=2016 | ||
| C. | ?x0∈R,sinx0+cosx0=$\sqrt{3}$ | D. | ?x∈R,2x>0 |
11.双曲线 $\frac{x^2}{4}-\frac{y^2}{16}=1$的一条渐近线方程为( )
| A. | y=2x | B. | $y=\frac{1}{2}x$ | C. | y=4x | D. | $y=\frac{1}{4}x$ |
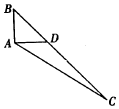 如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AC}$•$\overrightarrow{AD}$的值为( )
如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AC}$•$\overrightarrow{AD}$的值为( )