题目内容
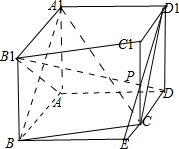
 如图,已知直四棱柱ABCD-A1B1C1D1的底面为直角梯形,AB∥CD,AB⊥AD,AB=AD=AA1=2CD=2,点P为棱CC1的中点.
如图,已知直四棱柱ABCD-A1B1C1D1的底面为直角梯形,AB∥CD,AB⊥AD,AB=AD=AA1=2CD=2,点P为棱CC1的中点.(Ⅰ)求证:D1P∥平面A1BC;
(Ⅱ)求证:D1P⊥平面AB1D;
(Ⅲ)求异面直线A1C与D1P所成的角.
考点:直线与平面平行的判定,异面直线及其所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)要证D1P∥平面A1BC,根据线面平行的判定定理,只要D1P平行于平面A1BC内一条直线即可,延长D1P,CD交于E,证明D1E∥A1B即可.
(Ⅱ)证明D1P垂直于平面AB1D内两条相交直线即可,容易证明D1P⊥AD,D1P⊥AB1.
(Ⅲ)先找出异面直线所成角,容易判断∠BA1C即为异面直线所成角,想办法求出△A1BC三条边的长度,根据余弦定理即可求所成角的余弦值,从而求出这个所成角.
(Ⅱ)证明D1P垂直于平面AB1D内两条相交直线即可,容易证明D1P⊥AD,D1P⊥AB1.
(Ⅲ)先找出异面直线所成角,容易判断∠BA1C即为异面直线所成角,想办法求出△A1BC三条边的长度,根据余弦定理即可求所成角的余弦值,从而求出这个所成角.
解答:
解:(Ⅰ)如图,延长DC,D1P相交于点E,连接BE;
 ∵P为CC1中点,且PC∥DD1;
∵P为CC1中点,且PC∥DD1;
∴PC=
DD1,DE=2CD=AB,AB∥CD;
∴四边形ABED为平行四边形;
∴AD∥BE∥A1D1,且AD=BE=A1D1;
∴四边形A1BED1是平行四边形;
∴D1E∥A1B,即D1P∥A1B,A1B?平面A1BC,D1P?平面A1BC;
∴D1P∥平面A1BC.
(Ⅱ)∵D1D⊥底面ABCD,AD?平面ABCD;
∴D1D⊥AD,即AD⊥D1D;
又AD⊥CD,D1D平面D1DE,CD?平面D1DE,且CD∩D1D=D;
∴AD⊥平面D1DE,D1E?平面D1DE;
∴AD⊥D1E,即D1P⊥AD;
∵A1B1BA是正方形;
∴A1B⊥AB1,∴D1P⊥AB1,AB1∩AD=A;
∴D1P⊥平面AB1D.
(Ⅲ)∵D1P∥A1B,∴∠BA1C是异面直线A1C与D1P所成的角;
连接CD1,则△A1CD1是Rt△;
A1D1=2,CD1=
,∴A1C=3;
A1B=2
,BC=
;
∴由余弦定理得:cos∠BA1C=
=
;
∴∠BA1C=45°,即异面直线A1C与D1P所成的角为45°.
 ∵P为CC1中点,且PC∥DD1;
∵P为CC1中点,且PC∥DD1;∴PC=
| 1 |
| 2 |
∴四边形ABED为平行四边形;
∴AD∥BE∥A1D1,且AD=BE=A1D1;
∴四边形A1BED1是平行四边形;
∴D1E∥A1B,即D1P∥A1B,A1B?平面A1BC,D1P?平面A1BC;
∴D1P∥平面A1BC.
(Ⅱ)∵D1D⊥底面ABCD,AD?平面ABCD;
∴D1D⊥AD,即AD⊥D1D;
又AD⊥CD,D1D平面D1DE,CD?平面D1DE,且CD∩D1D=D;
∴AD⊥平面D1DE,D1E?平面D1DE;
∴AD⊥D1E,即D1P⊥AD;
∵A1B1BA是正方形;
∴A1B⊥AB1,∴D1P⊥AB1,AB1∩AD=A;
∴D1P⊥平面AB1D.
(Ⅲ)∵D1P∥A1B,∴∠BA1C是异面直线A1C与D1P所成的角;
连接CD1,则△A1CD1是Rt△;
A1D1=2,CD1=
| 5 |
A1B=2
| 2 |
| 5 |
∴由余弦定理得:cos∠BA1C=
| 8+9-5 | ||
12
|
| ||
| 2 |
∴∠BA1C=45°,即异面直线A1C与D1P所成的角为45°.
点评:本题考查线面平行的判定定理,平行四边形的判定,线面垂直的性质,正方形的对角线相互垂直,线面垂直的判定定理,异面直线所成角,余弦定理.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
若S={1,2,3,4,5},M={1,3,4},N={2,4,5},则(∁SM)∩(∁SN)等于( )
| A、{1,3} | B、∅ |
| C、{4} | D、{2,5} |
 某班同学进行了一次数学测试,将所得的数据整理后,画出频率分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,且第一小组的频数是5.
某班同学进行了一次数学测试,将所得的数据整理后,画出频率分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,且第一小组的频数是5. 已知正三棱柱ABC-A1B1C1中,AB=2,AA1=
已知正三棱柱ABC-A1B1C1中,AB=2,AA1=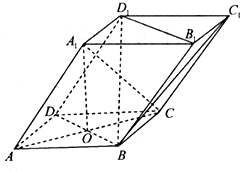 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2