题目内容
19.函数f(x)=ln(x2-x+1)-$\frac{2}{|2x-1|}$的所有零点的和为( )| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 由f(x)=ln[(x-$\frac{1}{2}$)2+$\frac{3}{4}$]-$\frac{1}{{|x-\frac{1}{2}|}}$,它是由偶函数g(x)=ln(x2+$\frac{3}{4}$)-$\frac{1}{|x|}$的图象向右平移$\frac{1}{2}$个单位得到,故f(x)的图象关于x=$\frac{1}{2}$对称,根据偶函数的性质,函数f(x)的所有零点的和x1+x2=2×$\frac{1}{2}$=1.
解答 解:f(x)=ln[(x-$\frac{1}{2}$)2+$\frac{3}{4}$]-$\frac{1}{{|x-\frac{1}{2}|}}$,
它是由偶函数g(x)=ln(x2+$\frac{3}{4}$)-$\frac{1}{|x|}$的图象向右平移$\frac{1}{2}$个单位得到,
故f(x)的图象关于x=$\frac{1}{2}$对称,
又g(x)在(0,+∞)上为增函数,
画图知g(x)有两个零点,如图示: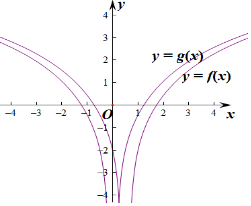
故f(x)有两个零点,
由g(x)有两个零点,两个零点关于y轴对称,则两个零点之和为0,
∴f(x)=ln(x2-x+1)-$\frac{2}{|2x-1|}$的所有零点的和x1+x2=2×$\frac{1}{2}$=1,
故选B.
点评 本题考查函数的图象变换,考查偶函数的性质,函数零点的应用,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
14.各项都是正数的等比数列{an}的公比q≠1,${a_1},\frac{1}{2}{a_3},{a_2}_{\;}$成等差数列,则$\frac{{{a_3}+{a_4}}}{{{a_4}+{a_5}}}$=( )
| A. | $\frac{{-1+\sqrt{3}}}{2}$ | B. | $\frac{{-1+\sqrt{5}}}{2}$ | C. | $\frac{{1+\sqrt{5}}}{2}$ | D. | $2+\sqrt{5}$ |
11.将函数f(x)=sin(x+$\frac{π}{6}$)的图象向左平移$\frac{π}{4}$个单位,所得函数g(x)图象的一个对称中心可以是( )
| A. | ($\frac{π}{12}$,0) | B. | (-$\frac{π}{12}$,0) | C. | ($\frac{7π}{12}$,0) | D. | (-$\frac{π}{4}$,0) |