题目内容
已知α∈(
,
),β∈(0,
),且cos(
-α)=
,sin(
π+β)=-
求cos(α+β).
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
| 5 |
| 4 |
| 12 |
| 13 |
∵sin(
π+β)=-sin(
+β)=-
∴sin(
+β)=
∵β∈(0,
),
∴cos(
+β)=
∵α∈(
,
),cos(
-α)=
∴sin(
-α)=
cos(α+β)=cos[(
+β)-(
-α)]=
×
+
×
=
| 5 |
| 4 |
| π |
| 4 |
| 12 |
| 13 |
∴sin(
| π |
| 4 |
| 12 |
| 13 |
∵β∈(0,
| π |
| 4 |
∴cos(
| π |
| 4 |
| 5 |
| 13 |
∵α∈(
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
∴sin(
| π |
| 4 |
| 4 |
| 5 |
cos(α+β)=cos[(
| π |
| 4 |
| π |
| 4 |
| 5 |
| 13 |
| 3 |
| 5 |
| 12 |
| 13 |
| 4 |
| 5 |
| 63 |
| 65 |

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 |=4,|
|=4,| |=3,
|=3, ,
, 
 |
| |=4,|
|=4,| |=3,(2
|=3,(2 =(2,5),
=(2,5), =(3,1),
=(3,1), =(6,3),在
=(6,3),在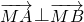 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由. |=4,|
|=4,| |=3,(2
|=3,(2 ﹣3
﹣3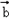 )(2
)(2 +
+ )=61,求
)=61,求 与
与 的夹角θ;
的夹角θ; =(2,5),
=(2,5), =(3,1),
=(3,1), =(6,3),在
=(6,3),在 上是否存在点M,使
上是否存在点M,使 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由.