题目内容
已知α∈(
,
),sin(α+
)=
,则tanα等于( )
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| 4 |
| 5 |
分析:由α的范围求出α+
的范围,根据sin(α+
)的值,利用同角三角函数间的基本关系求出cos(α+
)的值,进而确定出tan(α+
)的值,原式中的角α变形为(α+
)-
,利用两角和与差的正切函数公式化简后,将各自的值代入计算即可求出值.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答:解:∵
<α<
,∴
<α+
<π,
∵sin(α+
)=
,
∴cos(α+
)=-
=-
,
∴tan(α+
)=-
,
∴tanα=tan[(α+
)-
]=
=
=7.
故选B
| π |
| 4 |
| 3π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∵sin(α+
| π |
| 4 |
| 4 |
| 5 |
∴cos(α+
| π |
| 4 |
1-sin2(α+
|
| 3 |
| 5 |
∴tan(α+
| π |
| 4 |
| 4 |
| 3 |
∴tanα=tan[(α+
| π |
| 4 |
| π |
| 4 |
tan(α+
| ||||
1+tan(α+
|
-
| ||
1-
|
故选B
点评:此题考查了两角和与差的正切函数公式,同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 |=4,|
|=4,| |=3,
|=3, ,
, 
 |
| |=4,|
|=4,| |=3,(2
|=3,(2 =(2,5),
=(2,5), =(3,1),
=(3,1), =(6,3),在
=(6,3),在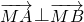 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由. |=4,|
|=4,| |=3,(2
|=3,(2 ﹣3
﹣3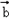 )(2
)(2 +
+ )=61,求
)=61,求 与
与 的夹角θ;
的夹角θ; =(2,5),
=(2,5), =(3,1),
=(3,1), =(6,3),在
=(6,3),在 上是否存在点M,使
上是否存在点M,使 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由.