题目内容
(1)已知| |=4,|
|=4,| |=3,(2
|=3,(2 -3
-3 )•(2
)•(2 +
+ )=61,求
)=61,求 与
与 的夹角θ;
的夹角θ;
(2)设 =(2,5),
=(2,5), =(3,1),
=(3,1), =(6,3),在
=(6,3),在 上是否存在点M,使
上是否存在点M,使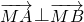 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由.
解:(1)∵(2 -3
-3 )•(2
)•(2 +
+ )=61
)=61
∴
又∵| |=4,|
|=4,| |=3
|=3
∴ •
• =-6.…3分
=-6.…3分
∴
∴θ=120°.…6分
(2)设存在点M,且
∴ .…8分
.…8分
∵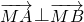
∴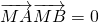
∴(2-6λ)(3-6λ)+(5-3λ)(1-3λ)=0,…10分
∴
∴
∴存在M(2,1)或 满足题意.…16分.
满足题意.…16分.
分析:(1)根据(2 -3
-3 )•(2
)•(2 +
+ )=61求出
)=61求出 •
• =-6然后再利用向量的夹角公式cos<
=-6然后再利用向量的夹角公式cos< >=
>= 再结合<
再结合< >∈[0,π]即可求出
>∈[0,π]即可求出 与
与 的夹角θ.
的夹角θ.
(2)假设存在点M符合题意则可设 即M(6λ,3λ)从而求出
即M(6λ,3λ)从而求出 再根据
再根据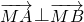 利用向量数量积的坐标计算再结合0<λ≤1即可求出λ进而求出点M.
利用向量数量积的坐标计算再结合0<λ≤1即可求出λ进而求出点M.
点评:本题主要考查了利用数量积求向量的夹角,属常考题,较易.解题的关键是熟记向量的夹角公式cos< >=
>= 同时要注意<
同时要注意< >∈[0,π]这一隐含条件以及
>∈[0,π]这一隐含条件以及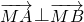 的等价条件
的等价条件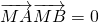 !
!
 -3
-3 )•(2
)•(2 +
+ )=61
)=61∴

又∵|
 |=4,|
|=4,| |=3
|=3∴
 •
• =-6.…3分
=-6.…3分∴

∴θ=120°.…6分
(2)设存在点M,且

∴
 .…8分
.…8分∵
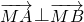
∴
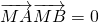
∴(2-6λ)(3-6λ)+(5-3λ)(1-3λ)=0,…10分
∴

∴

∴存在M(2,1)或
 满足题意.…16分.
满足题意.…16分.分析:(1)根据(2
 -3
-3 )•(2
)•(2 +
+ )=61求出
)=61求出 •
• =-6然后再利用向量的夹角公式cos<
=-6然后再利用向量的夹角公式cos< >=
>= 再结合<
再结合< >∈[0,π]即可求出
>∈[0,π]即可求出 与
与 的夹角θ.
的夹角θ.(2)假设存在点M符合题意则可设
 即M(6λ,3λ)从而求出
即M(6λ,3λ)从而求出 再根据
再根据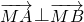 利用向量数量积的坐标计算再结合0<λ≤1即可求出λ进而求出点M.
利用向量数量积的坐标计算再结合0<λ≤1即可求出λ进而求出点M.点评:本题主要考查了利用数量积求向量的夹角,属常考题,较易.解题的关键是熟记向量的夹角公式cos<
 >=
>= 同时要注意<
同时要注意< >∈[0,π]这一隐含条件以及
>∈[0,π]这一隐含条件以及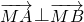 的等价条件
的等价条件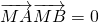 !
! 
练习册系列答案
相关题目
 |=4,|
|=4,| |=3,(2
|=3,(2 ﹣3
﹣3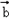 )(2
)(2 +
+ )=61,求
)=61,求 与
与 的夹角θ;
的夹角θ; =(2,5),
=(2,5), =(3,1),
=(3,1), =(6,3),在
=(6,3),在 上是否存在点M,使
上是否存在点M,使 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由.