题目内容
已知x>0,y>0,且4x+2y-xy=0,则x+y的最小值为 .
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:等式4x+2y-xy=0,可得
+
=1,则x+y=(x+y)(
+
),根据基本不等式即可得到答案.
| 2 |
| x |
| 4 |
| y |
| 2 |
| x |
| 4 |
| y |
解答:
解:已知x>0,y>0,且4x+2y-xy=0,可得
+
=1.
利用基本不等式:则x+y=(x+y)(
+
)=6+
+
≥6+4
,当且仅当
=
时成立.
则x+y的最小值为6+4
.
故答案为6+4
.
| 2 |
| x |
| 4 |
| y |
利用基本不等式:则x+y=(x+y)(
| 2 |
| x |
| 4 |
| y |
| 2y |
| x |
| 4x |
| y |
| 2 |
| 2y |
| x |
| 4x |
| y |
则x+y的最小值为6+4
| 2 |
故答案为6+4
| 2 |
点评:此题主要考查基本不等式的应用问题,题中凑基本不等式是解题的关键,有一定的技巧性,但覆盖的知识点较少,属于基础题目.

练习册系列答案
相关题目
算法的三要素不包括以下( )
| A、明确性 | B、有限性 |
| C、有序性 | D、模糊性 |
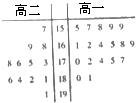 某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.
某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.