题目内容
17.f(x)=lg(sinx-cosx)的定义域是(2kπ+$\frac{π}{4}$,2kπ+$\frac{5π}{4}$)(k∈Z).分析 先将问题等价为:sinx>cosx,再根据三角函数线得出原函数的定义域.
解答 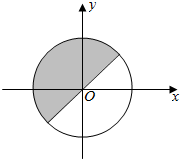 解:要使函数式f(x)=lg(sinx-cosx)有意义,
解:要使函数式f(x)=lg(sinx-cosx)有意义,
只需满足,sinx-cosx>0,
即sinx>cosx,
根据三角函数线可知,如右图(不含边界),
当角的终边在直线y=x上方时,符合题意,
此时,2kπ+$\frac{π}{4}$<x<2kπ+$\frac{5π}{4}$,
即函数f(x)的定义域为:(2kπ+$\frac{π}{4}$,2kπ+$\frac{5π}{4}$)(k∈Z),
故答案为:(2kπ+$\frac{π}{4}$,2kπ+$\frac{5π}{4}$)(k∈Z).
点评 本题主要考查了函数定义域的求法,涉及运用三角函数线比较三角函数值的大小,以及角的范围的表示方法,属于基础题.

练习册系列答案
相关题目
12.极限$\underset{lim}{x→0}$$\frac{1}{2+{3}^{\frac{1}{x}}}$的结果是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | 不存在 |
2.已知直线l经过椭圆$\frac{x^2}{169}$+$\frac{y^2}{144}$=1的右焦点,与椭圆交于A(x1,y1)、B(x2,y2),若x1+x2=1,则直线l的方程为( )
| A. | 4x-13y-20=0或4x+13y-20=0 | B. | 2x-3y-10=0或2x+3y-10=0 | ||
| C. | 6x+5y-30=0或6x-5y-30=0 | D. | 4x+9y-20=0或2x+3y-10=0. |
6.设$A=\left\{{x|y=\sqrt{1-{x^2}}}\right\},B=\left\{{y|y=lg({1-{x^2}})}\right\}$,则A∩B=( )
| A. | {(-1,1)} | B. | {(0,1)} | C. | [-1,0] | D. | [0,1] |
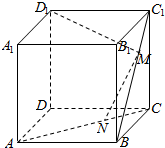 如图,正方体ABCD-A1B1C1D1的棱长为a,$\frac{AN}{NC}=\frac{BM}{{M{C_1}}}=3$.
如图,正方体ABCD-A1B1C1D1的棱长为a,$\frac{AN}{NC}=\frac{BM}{{M{C_1}}}=3$.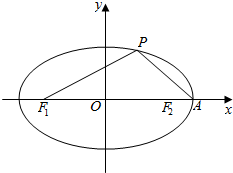 如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$
如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$