题目内容
6.设$A=\left\{{x|y=\sqrt{1-{x^2}}}\right\},B=\left\{{y|y=lg({1-{x^2}})}\right\}$,则A∩B=( )| A. | {(-1,1)} | B. | {(0,1)} | C. | [-1,0] | D. | [0,1] |
分析 分别求出两个函数的定义域和值域得到集合A,B,结合集合的交集运算定义,可得答案.
解答 解:∵由1-x2≥0得:x∈[-1,1],
∴A=[-1,1],
∵y=lg(1-x2)≤lg1=0得:
∴B=(-∞,0],
∴A∩B=[-1,0],
故选:C
点评 本题考查的知识点是集合的交集运算,求出A,B两个集合是解答的关键.

练习册系列答案
相关题目
16.下列函数既是偶函数,又在(0,+∞)上单调递增的是( )
| A. | y=-x2 | B. | y=x3 | C. | y=log2|x| | D. | y=-3-x |
18.在三角形ABC中,A=120°,AB=4,$BC=2\sqrt{19}$,则$\frac{sinB}{sinC}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{19}}}{2}$ | D. | $\frac{{2\sqrt{19}}}{19}$ |
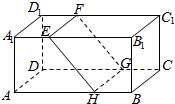 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.