题目内容
12.极限$\underset{lim}{x→0}$$\frac{1}{2+{3}^{\frac{1}{x}}}$的结果是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | 不存在 |
分析 分两类讨论,求出函数在x=0处的左右极限,由于左右极限不相等,得出该极限不存在.
解答 解:根据题意,分两类讨论如下:
①x→0+时,$\frac{1}{x}$→+∞,${3}^{\frac{1}{x}}$→+∞,
所以,$\underset{lim}{x→{0}^{+}}$$\frac{1}{2+{3}^{\frac{1}{x}}}$=0;
①x→0-时,$\frac{1}{x}$→-∞,${3}^{\frac{1}{x}}$→0,
所以,$\underset{lim}{x→{0}^{-}}$$\frac{1}{2+{3}^{\frac{1}{x}}}$=$\frac{1}{2}$;
由于,$\underset{lim}{x→{0}^{+}}$$\frac{1}{2+{3}^{\frac{1}{x}}}$≠$\underset{lim}{x→{0}^{-}}$$\frac{1}{2+{3}^{\frac{1}{x}}}$,
所以,极限$\underset{lim}{x→0}$$\frac{1}{2+{3}^{\frac{1}{x}}}$不存在,
故答案为:D.
点评 本题主要考查了极限及其运算,涉及函数在某点处的左右极限,以及极限存在的条件,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.一个年级共有12个班,每个班学生的学号从1到50,为交流学习经验,要求每班学号为14的同学留下,这里运用的是( )
| A. | 分层抽样法 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
20.设U={1,2,3,4},M={2,3},N={2,3,4},则(∁UM)∩N=( )
| A. | {1,4} | B. | {2,3} | C. | {4} | D. | {2,4} |
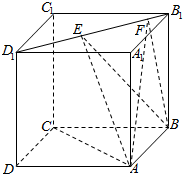 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )