题目内容
设集合A={(x,y)|y=x2+mx+2},B={(x,y)|x-y+1=0,0≤x≤2},若A∩B≠ϕ,则实数m的取值范围是 .
考点:交集及其运算
专题:函数的性质及应用,集合
分析:联立方程组
,得x2+(m-1)x+1=0,由已知方程x2+(m-1)x+1=0在[0,2]上有实数根.由此能求出m的取值范围.
|
解答:
解:联立方程组
,
得x2+(m-1)x+1=0,
∵A∩B≠∅,∴方程x2+(m-1)x+1=0在[0,2]上有实数根.
设f(x)=x2+(m-1)x+1,显然f(0)=1>0,
则由二次函数的性质,得:
f(2)≤0或
解得m≤-1.
∴所求m的取值范围是(-∞,-1].
故答案为:(-∞,-1].
|
得x2+(m-1)x+1=0,
∵A∩B≠∅,∴方程x2+(m-1)x+1=0在[0,2]上有实数根.
设f(x)=x2+(m-1)x+1,显然f(0)=1>0,
则由二次函数的性质,得:
f(2)≤0或
|
解得m≤-1.
∴所求m的取值范围是(-∞,-1].
故答案为:(-∞,-1].
点评:本题是数形结合思想?函数方程思想?化归思想等数学思想的综合运用.涉及到二次函数的问题,抓住函数的图象是关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
若a<b<0,则下列不等式中,一定成立的是( )
| A、a2<ab<b2 |
| B、a2>ab>b2 |
| C、a2<b2<ab |
| D、a2>b2>ab |
函数f(x)=x|x|-x3是 ( )
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
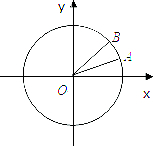 如图,在平面直角坐标系中xOy中,以轴Ox为始边做两个锐角α,β,它们的终边分别与单位圆相交于A.B两点,已知A,B的纵坐标分别为
如图,在平面直角坐标系中xOy中,以轴Ox为始边做两个锐角α,β,它们的终边分别与单位圆相交于A.B两点,已知A,B的纵坐标分别为