题目内容
1.函数y=$\sqrt{x-1}$+1的值域为( )| A. | (0,+∞) | B. | (1,+∞) | C. | [0,+∞) | D. | [1,+∞) |
分析 由题意可得出函数y=$\sqrt{x-1}$+1是增函数,由单调性即可求值域.
解答 解:函数y=$\sqrt{x-1}$+1,定义域为[1,+∞),
根据幂函数性质可知,函数y为增函数,
当x=1时,函数y取得最小值为1,
函数y=$\sqrt{x-1}$+1的值域为[1,+∞),
故选D
点评 本题考查幂函数的单调性,属于函数性质应用题求解值域问题,较容易.

练习册系列答案
相关题目
11.已知平面向量$\overrightarrow a=(-2,1)$,$\overrightarrow b=(1,2)$,则$|{\overrightarrow a-2\overrightarrow b}|$的值是( )
| A. | 1 | B. | 5 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
16.圆的任何一对平行切线间的距离总是相等的,即圆在任意方向都有相同的宽度,具有这种性质的曲线可称为“等宽曲线”.事实上存在着大量的非圆等宽曲线,以工艺学家鲁列斯( Reuleaux)命名的鲁列斯曲边三角形,就是著名的非圆等宽曲线.它的画法(如图1):画一个等边三角形ABC,分别以A,B,C为圆心,边长为半径,作圆弧$\widehat{BC},\widehat{CA},\widehat{AB}$,这三段圆弧围成的图形就是鲁列斯曲边三角形.它的宽度等于原来等边三角形的边长.等宽曲线都可以放在边长等于曲线宽度的正方形内(如图2).

在图2中的正方形内随机取一点,则这一点落在鲁列斯曲边三角形内的概率为( )

在图2中的正方形内随机取一点,则这一点落在鲁列斯曲边三角形内的概率为( )
| A. | $\frac{π}{8}$ | B. | $\frac{{2π-3\sqrt{3}}}{4}$ | C. | $\frac{{π-\sqrt{2}}}{2}$ | D. | $\frac{{π-\sqrt{3}}}{2}$ |
6.已知三棱锥A-BCD的四个顶点A,B,C,D都在球O的表面上,BC⊥CD,AC⊥平面BCD,且AC=2$\sqrt{2}$,BC=CD=2,则球O的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 2$\sqrt{2}$π |
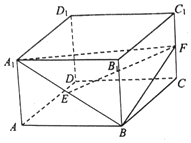 如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.
如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.