题目内容
20.设m∈R,实数x,y满足$\left\{\begin{array}{l}{y≥m}\\{2x-3y+6≥0}\\{3x-2y-6≤0}\end{array}\right.$,若|2x+y|≤18恒成立,则实数m的取值范围是( )| A. | -3≤m≤3 | B. | -6≤m≤6 | C. | -3≤m≤6 | D. | -6≤m≤0 |
分析 将不等式恒成立问题转化为平面区域在两条直线之间利用数形结合进行求解即可.
解答 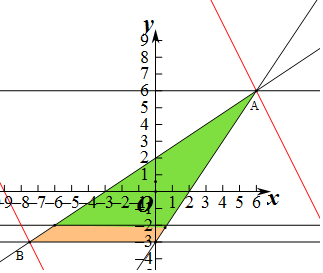 解:由|2x+y|≤18得-18≤2x+y≤18,
解:由|2x+y|≤18得-18≤2x+y≤18,
若|2x+y|≤18恒成立,
等价为不等式组对应的平面区域
都在直线2x+y=18和2x+y=-18之间,
即对应的两个直线(红色)之间,
作出不等式组对应的平面区域如图,
由$\left\{\begin{array}{l}{2x-3y+6=0}\\{3x-2y-6=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=6}\\{y=6}\end{array}\right.$,即A(6,6),此时A满足条件.2x+y=18,
由$\left\{\begin{array}{l}{2x-3y+6=0}\\{2x+y=-18}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{15}{2}}\\{y=-3}\end{array}\right.$,
即B(-$\frac{15}{2}$,-3),
要使不等式组对应的平面区域都在两条直线之间,
则直线y=m满足在直线y-=-3和y=6之间,
则-3≤m≤6,
故选:C
点评 本题主要考查线性规划的应用,将不等式恒成立转化为平面区域在两条直线之间是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
11.已知平面向量$\overrightarrow a=(-2,1)$,$\overrightarrow b=(1,2)$,则$|{\overrightarrow a-2\overrightarrow b}|$的值是( )
| A. | 1 | B. | 5 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
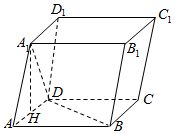 四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AD=AA1=A1D=2,H为AD中点,且A1H⊥BD.
四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AD=AA1=A1D=2,H为AD中点,且A1H⊥BD.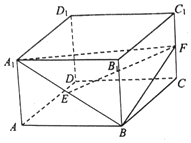 如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.
如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.