题目内容

已知函数f（x）=
2x-2，x≤1
2+log2x，x＞1
，则函数f（x）的零点为（　　）
A、
1
4
和1
B、-4和0
C、
1
4
D、1
考点：函数零点的判定定理
专题：函数的性质及应用
分析：直接解方程f（x）=0即可．
解答： 解：若x＞1，则由f（x）=0得，2+log2x=0，即log2x=-2，解得x=
1
4
，此时无解，
若x≤1，则由f（x）=0得，2x-2=0，解得x=1，
故函数f（x）的零点为1，
故选：D．
点评：本题主要考查函数零点的求解，直接解方程是解决本题的关键．
练习册系列答案
相关题目
已知sinα+sinβ=
6
3
，cosα-cosβ=
3
3
，则cos2
α+β
2
=
 
．
给出下列结论：
①“a＞b”是“a2＞b2”的充分条件；
②若p：?x∈R，x2+2x+2＞0，则￢p：?x0∈R，x02+2x0+2≤0；
③“若m＞0，则方程x2+x-m=0有实数根”的否命题是“若m≤0，则方程x2+x-m=0没有实数根”；
④若p∧q是假命题，则p、q均为假命题．
则其中正确结论的序号是（　　）
A、①②B、①③C、②③D、③④
函数y=sin2x的一个单调递增区间可以是（　　）
A、[-
π
4
，
π
4
]
B、[-
π
2
，
π
2
]
C、[
π
2
，
3π
4
]
D、[0，π]
把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半，纵坐标扩大到原来的两倍，然后把图象向左平移
π
4
个单位，则所得图形表示的函数的解析式为（　　）
A、y=2sin2x
B、y=-2sin2x
C、y=2cos（x+
π
4
）
D、y=2cos（
x
2
+
π
4
）
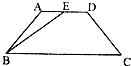如图，在等腰梯形ABCD中，下底BC长为3，底角C为45°，高为a，E为上底AD的中点，F为折线段C-D-A上的动点，设
BE
•
BF
的最小值为g（a），若关于a的方程g（a）=ka-1有两个不相等的实根，则实数k的取值范围为（　　）
A、（
7
2
，
11
3
）
B、（
7
2
，+∞）
C、（
11
3
，+∞）
D、（
13
，+∞）
在二项式（1+x）n的展开式中，存在系数之比为2：3的相邻两项，则指数n（n∈N+）的最小值为（　　）
A、6B、5C、4D、3
已知角α终边上一点P（-4a，3a）（a＜0），则sinα的值为（　　）
A、
3
5
B、-
4
5
C、
4
5
D、-
3
5
从6名班委中选出2人分别担任正、副班长，一共有多少种选法？（　　）
A、11B、12C、30D、36

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网