题目内容
如图,在复平面内,复数z1和z2对应的点分别是A和B,则
=( )

| z1 |
| z2 |

A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的几何意义、运算法则即可得出.
解答:
解:由图可知:z1=i,z2=2-i,
则则
=
=
=
=-
+
i.
故选:D.
则则
| z1 |
| z2 |
| i |
| 2-i |
| i(2+i) |
| (2-i)(2+i) |
| -1+2i |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
故选:D.
点评:本题考查复数的除法运算、几何意义,属于基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
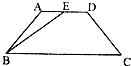 如图,在等腰梯形ABCD中,下底BC长为3,底角C为45°,高为a,E为上底AD的中点,F为折线段C-D-A上的动点,设
如图,在等腰梯形ABCD中,下底BC长为3,底角C为45°,高为a,E为上底AD的中点,F为折线段C-D-A上的动点,设| BE |
| BF |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
已知直线a与直线b是异面直线,过空间一定点P(点P不在直线a与直线b上)作与直线a、直线b都平行的平面有( )
| A、有且只有一个 |
| B、不存在或者有一个 |
| C、有无数个 |
| D、恰有两个 |
已知全集为R,A={x|y=
},B={x||x-2|<1},则(∁RA)∩B=( )
| 1 | ||
|
| A、[1,2] |
| B、(1,2] |
| C、[0,3] |
| D、(0,3) |
从6名班委中选出2人分别担任正、副班长,一共有多少种选法?( )
| A、11 | B、12 | C、30 | D、36 |
函数y=
(x≠
)的图象与函数y=
+
(x≠0)的图象关于( )
| 1 |
| 2x-1 |
| 1 |
| 2 |
| 1 |
| 2x |
| 1 |
| 2 |
| A、y轴对称 | B、x轴对称 |
| C、y=x对称 | D、原点对称 |
设函数f(x)=|lgx|,若f(a)=f(b)(0<a<b),则
+
( )
| 1 |
| a |
| 2 |
| b |
| A、有最小值3 | ||
| B、无最小值 | ||
C、有最小值2
| ||
| D、有最大值 |
 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD,M为AD中点,AB=BD=CD=1.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD,M为AD中点,AB=BD=CD=1.