题目内容
已知直线l:x-y+4=0与圆C:(x-1)2+(y-1)2=2,则圆C上各点到l的距离的最小值为( )
A、
| ||
B、
| ||
| C、1 | ||
| D、3 |
考点:直线与圆的位置关系
专题:直线与圆
分析:圆C上各点到l的距离的最小值为圆心到直线的距离减去半径.
解答:
解:∵圆C:(x-1)2+(y-1)2=2的圆心C(1,1),半径r=
,
圆心C(1,1)到直线的距离d=
=2
,
∴圆C上各点到l的距离的最小值为:
d-r=2
-
=
.
故选:A.
| 2 |
圆心C(1,1)到直线的距离d=
| |1-1+4| | ||
|
| 2 |
∴圆C上各点到l的距离的最小值为:
d-r=2
| 2 |
| 2 |
| 2 |
故选:A.
点评:本题考查圆C上各点到l的距离的最小值的求法,是基础题,解题时要认真审题,注意直线与圆的位置关系的合理运用.

练习册系列答案
相关题目
设m,n是两条不同的直线,α,β,γ是三个不同的平面.有下列四个命题:
①若m?β,α⊥β,则m⊥α
②若α∥β,m?α,则m∥β
③若n⊥α,n⊥β,m⊥α则m⊥β
④若α⊥γ,β⊥γ,则α⊥β
其中正确命题的序号是( )
①若m?β,α⊥β,则m⊥α
②若α∥β,m?α,则m∥β
③若n⊥α,n⊥β,m⊥α则m⊥β
④若α⊥γ,β⊥γ,则α⊥β
其中正确命题的序号是( )
| A、①③ | B、①② | C、③④ | D、②③ |
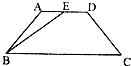 如图,在等腰梯形ABCD中,下底BC长为3,底角C为45°,高为a,E为上底AD的中点,F为折线段C-D-A上的动点,设
如图,在等腰梯形ABCD中,下底BC长为3,底角C为45°,高为a,E为上底AD的中点,F为折线段C-D-A上的动点,设| BE |
| BF |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
执行如图所示的程序框图,则输出的结果是( )


| A、14 | B、15 | C、16 | D、17 |
已知角α终边上一点P(-4a,3a)(a<0),则sinα的值为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知cosθ=cos30°,则θ等于( )
| A、30° |
| B、k•360°+30°(k∈Z) |
| C、k•360°±30°(k∈Z) |
| D、k•180°+30°(k∈Z) |
已知直线a与直线b是异面直线,过空间一定点P(点P不在直线a与直线b上)作与直线a、直线b都平行的平面有( )
| A、有且只有一个 |
| B、不存在或者有一个 |
| C、有无数个 |
| D、恰有两个 |
已知全集为R,A={x|y=
},B={x||x-2|<1},则(∁RA)∩B=( )
| 1 | ||
|
| A、[1,2] |
| B、(1,2] |
| C、[0,3] |
| D、(0,3) |
 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD,M为AD中点,AB=BD=CD=1.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD,M为AD中点,AB=BD=CD=1.